Жак Арсак - Программирование игр и головоломок

Потренируйтесь в доказательствах такого рода…

Игра 32.

Предыдущее рекурсивное решение имеет ту особенность, что она не включает в ход игры никакого представления этой игры. Если вы хотите представить игру на экране даже символическим образом, вам придется создавать представление игры самому.

Но трудность состоит только в осуществлении видимого представления, потому что нужно учесть все, сказанное выше. Предположим, что нужно выполнить Р ( р , н , к ). Вы знаете, что нужно осуществить движение, которое вводит в игру диск размера р , покидающий стержень н , с которого он отправляется на стержень к . Это означает, что диск р находится на вершине стержня к , в противном случае его нельзя было бы оттуда взять. Поэтому вы можете не обращать никакого внимания на значение р .

Операция Р ( р , н , к ) на самом деле следующая: снять диск с вершины стержня н и поместить его на вершину стержня к .

Если представить игру в виде 3 строк с помощью последовательностей чисел, то, таким образом, достаточно снять крайнее правое число со строки н и присоединить его справа к строке к .

Если вы хотите представить стержни вертикально, создайте, кроме того, внутреннее представление с помощью трех цепочек символов и составьте процедуру вывода на экран. Это, как кажется, проще всего. Если вы не любите цепочек символов, используйте три таблицы, но вы не выиграете в легкости.

Игра 33.

Если ваш компьютер допускает рекурсию, заставьте работать рекурсивную процедуру и понаблюдайте за движением дисков. В противном случае выполните вручную рекурсивную процедуру для маленького n (например 4), что поможет вам наглядно увидеть то, что уже доказано: два диска одинаковой четности не могут оказаться друг на друге.

Вы должны заметить, что

— диск с номером 1 перемещается один раз за любые два хода,

— он перемещается циклически, причем всегда в одном направлении, а именно

либо 0 — 1 1 — 2 2 — 0…

либо 0 — 2 2 — 1 1 — 0…

Следующий ход, перемещающий диск с номером 1, полностью определен. Недостаточно проверить это, это нужно доказать. После этого итеративное решение тривиально. Можете ли вы априори определить перемещение диска с номером 1 в зависимости от четности числа дисков?

Можете ли вы сказать что-нибудь о движении остальных дисков?

Пронумеруйте ходы. Диск с номером 1 перемещается в ходах с нечетными номерами. Проверьте, а затем докажите, что диск с номером 2 перемещается в ходах с номерами 2, 6, 10, …, т. е. в ходах, номер которых кратен двум, но не кратен четырем. Обобщите. Исходя отсюда, вы можете сказать, зная номер хода, какой диск будет перемещаться, с какого стержня он уйдет и куда придет.

Красиво, не правда ли?

Игра 34.

Существование четвертого стержня не упрощает стратегию, даже наоборот. Одна из возможностей состоит в том, чтобы перемещать р верхних дисков, используя 4 стержня, затем оставшиеся диски — используя только 3 стержня (поскольку четвертый стержень блокирован башней самых маленьких дисков). Наконец, вы восстанавливаете р маленьких дисков над остальными, используя 4 стержня. Обозначим через

f 4( р ) — число ходов для перемещения р дисков, используя 4 стержня;

f 3( р ) — число ходов для перемещения р дисков, используя 3 стержня (известное число, см. игру 31).

Тогда наша стратегия дает

f 4( n ) = f 4( р ) + f 3( n − p ) + f 4( р ).

Нужно выбрать значение р , которое минимизирует эту сумму.

Первые несколько значений для /4 получить легко:

f 4(1) = 1, f 4(2) = 3, f 4(3) = 5.

В этих случаях на самом деле есть только один способ действовать. Вычислите сначала на руках следующие значения. Воспользуйтесь вашим компьютером, чтобы составить таблицу, дающую последовательные значения для f 4( n ), вместе с оптимальным значением р для каждого n (оно не всегда однозначно определено. Вы по своему произволу можете выбирать из них наименьшее).

Игра 35.

Итеративная программа для игры с 4 стержнями есть обобщение итеративной программы для игры с 3 стержнями. Это видно по рекурсивной форме. Она не идеально проста…

Это замечание позволит вам перейти к любому числу стержней.

Игра 36.

Нужно снова взять все, что было нами оставлено в игре 23. Предположите, что для некоторого р существует такое значение q , что

SG( p , q ) = 0.

Покажите, что в этом случае SG( р , q ') = 0 для всех q ' < q . Следовательно, если р таково, что SG( р , 1) = 0, то должно существовать некоторое g такое, что SG( р , g ) = 0, но SG( р , g + 1) ≠ 0; g — наибольшее из значений q , дающих равенство SG( р , q ) = 0.

Нужно построить последовательность p i , g i .

Вы можете показать, что если g i = 1, то p i +1= p i + 2, в то время как если g i > 1, то p i +1= p i + 3.

Хороший способ действия состоит в том, чтобы опереться на геометрические рассмотрения. Числа Спрага-Грюнди интересуют нас только с одной стороны— равны они нулю или нет (у нас нет намерения играть несколько игр одновременно, что избавляет нас от вычисления Ним-сумм и, следовательно, от заботы о значениях ненулевых чисел Спрага-Грюнди). Число Спрага-Грюнди равно нулю тогда и только тогда, когда невозможен никакой переход к нулевому числу. Но положение р , q допускает переходы к p − k , для k ≤ 2 q . Следовательно, мы получим SG( p , q ) = 0 тогда и только тогда, когда

SG( p − k , k ) ≠ 0 для всех k от 1 до 2 q .

Нарисуйте на плоскости две перпендикулярные оси, p как абсциссу и q как ординату. Обозначьте точки с нулевыми значениями SG.

Рассмотрите те прямые, которые проходят через точки p c SG( p , 1) = 0. Нужно изучить прямые p − k , k , где меняется от 1, т. е. те, которые параллельны биссектрисе второго и четвертого координатного угла и проходят через точку p − 1, 1.

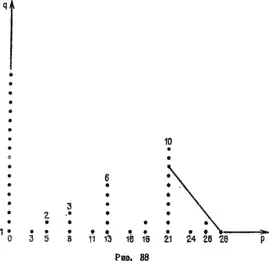
Мы представили отрезок такой прямой для p = 28 (см. рис. 38). Он пересекает точку с нулевым значением на вертикали 21 = 28 − 7. Значит, нужно ограничить число k шестью, задавая g = 3 при p = 28.

Для p = 34 диагональ, проходящая через 33, 1 проходит над всеми отрезками с 0 для p ≠ 0 и пройдет поэтому, пересекая ось q при q = 34. Поэтому нужно ограничить число k тридцатью тремя и, следовательно, взять g = 33 : 2 = 16.

У вас есть также некоторое число таких p i , что диагональ, выходящая из p i − 1, 1, не пересекает никакого отрезка нулей перед осью q , что дает g i = ( p i − 1) : 2.