Алексей Валиков - Технология XSLT

□ Если атрибут элемента был определен в DTD со значением по умолчанию, то в преобразовании нельзя точно сказать, присутствовал ли он физически во входящем документе или нет.

□ Не учитывается, был ли пустой элемент определен как или .

Одним словом, предложенная выше модель не учитывает информацию, которая не важна с точки зрения структуры документа. На практике помимо структуры бывает также важен и детальный синтаксис документа (например, необходимо вместо выводить ). К сожалению, применение XSLT для таких задач ограничено вследствие ограничений самой модели документа.

Узлы дерева XML-документа находятся в определенном порядке, который называется порядком просмотра документа (англ. document order). Этот порядок важен для вычисления XPath-вырэжений, которые оперируют множествами узлов. Несмотря на то, что эти множества не имеют внутреннего порядка, при вычислении выражений узлы в них будут перебираться в прямом или обратном порядке просмотра документа в зависимости от того, какие оси навигации применяются в выражении.

Порядок просмотра документа — это порядок, который соответствует появлению в документе первого символа текстовой записи узла. Например, для элементов это будет порядок появления в документе открывающих тегов.

Более четко порядок просмотра документа определяется следующими правилами:

□ корневой узел является первым узлом в порядке просмотра документа;

□ узлы элементов предшествуют своим дочерним узлам, узлам пространств имен и узлам атрибутов;

□ узлы пространств имен предшествуют узлам атрибутов;

□ узлы атрибутов предшествуют другим дочерним узлам своего элемента;

□ остальные узлы упорядочиваются в последовательности их появления в документе.

Обратным порядком просмотра документа называется порядок, который в точности противоположен обычному порядку просмотра документа. Обычный порядок просмотра документа также называют прямым порядком или порядком документа.

В качестве примера приведем схему дерева и выясним порядок просмотра

следующего документа:

<���а level="0" xmlns:b="urn:b" xmlns="urn:a">

alpha

delta

Дерево этого документа показано на рис. 3.11. Порядок просмотра данного документа будет следующим:

□ корневой узел;

□ узел комментария ;

□ узел инструкции по обработке ;

□ узел элемента a;

□ узел пространства имен "urn:а";

□ узел пространства имен "urn:b";

□ атрибут level;

□ текстовый узел " alpha";

□ узел элемента b:bravo;

□ узел пространства имен "urn:а";

□ узел пространства имен "urn:b";

□ комментарий с текстом " To do ...";

□ элемент charlie;

□ узел пространства имен "urn:а";

□ узел пространства имен "urn:b";

□ текстовый узел " delta";

□ узел инструкции по обработке .

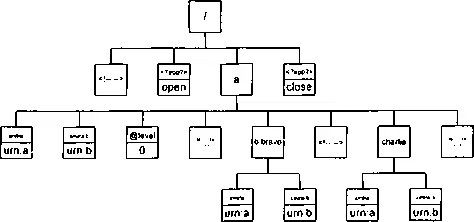
Рис. 3.11. Схема дерева XML-документа

Соответственно, обратный порядок просмотра документа будет начинаться с инструкции по обработке и заканчиваться корневым элементом.

Многие языки программирования при объявлении переменной требуют указывать, какой тип данных будет ей присваиваться. Например, в языке Java код

int i = 15;

объявит переменную целого типа intс именем iи присвоит ей значение 15. В этом случае тип данных ставится в соответствие переменной. XSLT относится к динамически типизируемым языкам, в которых тип данных ассоциируется не с переменными, а со значениями.

В XSLT выделяется пять типов данных:

□ булевый тип (boolean);

□ численный тип (number);

□ строковый тип (string);

□ множество узлов (node-set);

□ результирующий фрагмент дерева (result tree fragment).

Ниже мы подробно рассмотрим особенности работы со всеми пятью типами данных.

Булевый тип данных в XSLT может принимать два значения — true("истина") и false("ложь"). В XSLT нет констант для выражения тождественной "истины" или "лжи", как во многих других языках программирования, для этих целей следует использовать функции trueи false.

Значение булевого типа могут быть получены путем сравнения других типов данных при помощи операторов сравнения (таких как " =", " >", " <") или как результат вычисления более сложных логических выражений с использованием операторов " and", " or" и функции not.

Булевый тип может быть неявно преобразован в число ( 0для falseи 1для true) или в строку ( "false"и "true"соответственно).

Примеры:

1=2→ 0 (число)

not((2>1) and (2>3))→ "true" (строка)

Численный тип в XSLT определяется как 64-битное значение с плавающей точкой, двойной точности, соответствующее стандарту IEEE 754-1985. Этот стандарт используется во многих других языках программирования, и потому можно сказать, что арифметика в XSLT работает "как обычно". Вместе с тем, стандарт IEEE 754 имеет свои нюансы, которые обязательно надо учитывать в практике программирования на XSLT.

Согласно строгому определению, числа в XSLT имеют форму s× m×2 x , где s— знак числа, m— его мантисса, а x— экспонента. Эти числа имеют следующие значения:

□ знак ( s) равен +1для положительных чисел и -1для отрицательных;

□ мантисса ( m) — это положительное целое число в интервале от 0до 2 53-1включительно;

□ экспонента ( x) — это целое число в интервале от -1075до 970включительно.

Таким образом, числа в XSLT находятся в интервале приблизительно от -10 317до 10 317.

Кроме этого выделяются пять особых значений.

□ Отрицательная бесконечность. Это значение представляет отрицательные числа, меньшие, чем -10 317; оно соответствует математическому значению -∞. Отрицательная бесконечность может быть результатом таких операций, как деление отрицательного числа на нуль или умножение двух очень больших (в абсолютном значении) чисел разного знака в случае, когда для записи их произведения не хватит 64 бит.

□ Положительная бесконечность. Это значение представляет очень большие положительные числа, превосходящие 10 317; оно соответствует математическому значению ∞. Положительная бесконечность может быть результатом таких операций, как деление положительного числа на нуль или умножение двух очень больших (в абсолютном значении) чисел одного знака в случае, когда для записи их произведения не хватит 64 бит.