Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

то есть почти в 2 раза выше, чем у флеша. А шанс его получить – 1 к 250. Именно поэтому флеш в покере ценится больше: его куда сложнее собрать.

Еще более ценен фул-хаус – 3 карты одного достоинства плюс 2 карты другого. Что-то вроде этого [9]:

Чтобы подсчитать свои шансы на фул-хаус, нам сперва нужно выбрать необходимое нам достоинство, которое попадется нам трижды (13 вариантов), потом – то, которое попадется дважды (12 вариантов). Допустим, нам нужны 3 дамы и 2 семерки. Определимся с мастями. Получить нужных нам дам можно 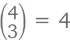способами, семерки – 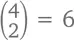способами. Общее количество фул-хаусов, таким образом, равняется

Следовательно, вероятность его собрать – 3744/2 598 960 или 1 к 700.

От фул-хаусов перейдем к двум парам . Здесь нам нужны две карты одного достоинства, еще две – другого, и последняя – третьего, например

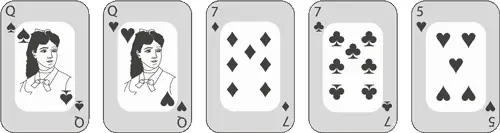
Пытаясь посчитать количество возможных пар, многие ошибочно начинают с 13 × 12, как в случае с фул-хаусами. Но теперь нам нужно немного другое, ведь здесь вероятность получить две семерки после двух дам – это абсолютно то же, что и получить двух дам после двух семерок. Поэтому правильно будет начать с 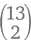(имея в виду и семерки, и дам), потом выбрать новое достоинство для непарной карты (пусть это будет пятерка), затем выбрать масти. Количество комбинаций с двумя парами –

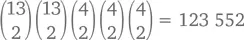
Появляются они в 5 % случаев.

Подробнее на всех вариантах раздач мы останавливаться не будем, но я попрошу вас взглянуть на следующие подсчеты и проверить, насколько они верны. Комбинаций с каре- [10], вроде 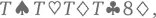может быть

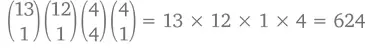
с тройкой- [11], например, –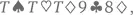

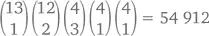
с одной парой – скажем, –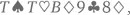

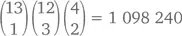
всего – 42 % всех возможных комбинаций.

А сколько же может быть «пустых» комбинаций – без пар, без стритов и без флешей? Можете, конечно, сложить все числа, которые мы получили до этого и вычесть сумму из 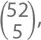но я облегчу вам жизнь и просто дам ответ:

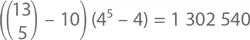
Первая часть – это количество комбинаций 5 карт разного достоинства за вычетом 10 последовательных (вроде 3-4-5-6-7). Следующая часть охватывает вероятные «расклады» этих 5 карт разного достоинства; для каждого достоинства у нас есть 4 варианта, но при этом мы должны исключить возможность того, что все они встретятся в одном «раскладе». Все это значит, что наши шансы собрать «пустую» комбинацию – 50,1 %. А еще это значит, что в 49,9 % случаев мы будем играть как минимум с одной парой.

А теперь вопрос, на который можно дать целых три прелюбопытных ответа, причем правильными из них будут сразу два! Сколько существует комбинаций, в которых есть как минимум один туз? Уверен, вас так и подмывает ответить что, само собой, неправильно . Вы же исходите (и напрасно) из того, что сначала нужно выбрать туза (4 варианта), а потом собирать любые другие 4 карты из 51 оставшейся в колоде. Неправильно здесь то, что вы таким образом просчитываете некоторые комбинации (а именно – те, в которых больше одного туза) несколько раз. Например, комбинация 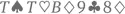будет посчитана дважды: сначала для Т ♠ в качестве первой, основной карты, а затем так же для Правильный способ решить эту задачу – разбить ее на четыре задачи поменьше, в зависимости от того, сколько тузов будет в комбинации. Так, комбинаций именно с одним тузом будет (сначала выбираем туза, потом – остальные 4 карты другого достоинства). Затем отдельно же просчитываем комбинации с двумя, тремя и четырьмя тузами. В результате получаем

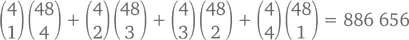
Но проще всего будет пойти от обратного . Сначала посчитаем количество комбинаций без туза (это легче легкого) – 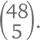А количество комбинаций по крайней мере с одним тузом, таким образом, –

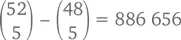
Я уже говорил чуть выше, что «цена» комбинаций в покере зависит от частоты их появлений: чем реже комбинация, тем она «ценнее». То есть если шансов собрать одну пару больше, чем сразу две, одна пара ценится куда меньше двух. Вот «стоимость» всех комбинаций, от меньшей к большей:

Пара

Две пары

Тройка

Стрит

Флеш

Фул-хаус

Каре (или «четверка»)

Стрит-флеш

На этот случай есть эффективная «запоминалка»: «Раз, два, три, стрит, флеш; два-три, четыре, стрит-флеш» (где «два-три» – это фул-хаус).

А теперь предположим, что в колоде появились джокеры. Всего карт у нас становится 54, причем джокеры (всего их два) могут «превращаться» в карту любой масти и любого достоинства – в зависимости от того, что вам нужно для наилучшей комбинации. То есть если у вас на руках 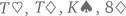и джокер, разумнее всего будет посчитать его тузом, чтобы получилась тузовая тройка. Можно «превратить» джокера и в короля, конечно, но тогда у вас будет две пары, что хуже, чем тройка [12].