Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Но здесь-то и начинается самое интересное. Следуя традиционному порядку карт, мы можем посчитать эту комбинацию и как тройку, и как две пары, а можем – только как тройку, исключив ее из числа двух пар. Последнее выглядит наиболее разумно, но ведь это значит, что общее количество комбинаций с тройками значительно увеличивается, а с двумя парами – уменьшается, что превращает последние в более редкие. Мы, конечно, можем сказать, что теперь две пары имеют бóльшую ценность, но проблему этим не решишь: она всего лишь «перевернется вверх ногами», ведь количество двух пар увеличится, а количество троек – уменьшится. Из этого всего следует странный на первый взгляд вывод, сделанный математиком Стивом Гэдбойсом в 1996 году: при игре в покер с джокерами невозможно ранжировать «ценность» комбинаций по частоте их появления.

Вот вам во всей его красе треугольник Паскаля:

Треугольники уже знакомы нам по главе 1, так что мы хорошо знаем, насколько интересные закономерности могут появляться из организованных таким образом чисел. Еще более интересные (и куда более красивые) закономерности получатся в треугольнике чисел 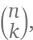о которых мы только что узнали. Такой треугольник называется Паскалевым – тот, который изображен чуть выше. У нас есть формула 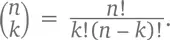Давайте превратим все ее символы в числа и поищем закономерности (см. изображение треугольника чуть ниже). Большинство из них будут подробно описаны в этой главе, но, если объяснения вдруг покажутся вам скучными, можете смело их пропускать и просто наслаждайтесь стройной красотой самих закономерностей.

Верхний (или нулевой) ряд представлен одним-единственным значением – 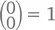(не забывайте: 0! = 1). Каждый ряд начинается с единицы и ею же заканчиваются, потому что

Взгляните на пятый ряд:

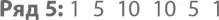
Обратите внимание, что второе число в нем – 5, да и в принципе вторым числом ряда n будет n . Это все из-за 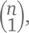за того, что количество способов выбрать один объект из множества n равно n . Также стоит обратить внимание, что каждый ряд

геометрически симметричен : чисел до центральной оси столько же, сколько и после нее. В том же самом 5 ряду мы видим

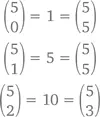
В целом же закономерность говорит о том, что

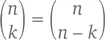
У таких симметричных отношений есть два объяснения. Первое – алгебраическое – с помощью формулы

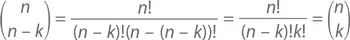
Но так ли уж сильно она нам тут нужна? Почему, например, 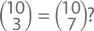Число обозначает количество вариантов выбора 3 сортов мороженого из десяти (в вазочке, не в рожке). Но ведь это то же самое, что считать варианты выбора тех 7 сортов, которые мы не купим.

Следующая закономерность, которую легко заметить, заключается в том, что во всех, кроме 1-го, рядах каждое число есть, по сути, сумма двух других – тех, которые находятся прямо над ним. Посмотрите, например, на 9 и 10 ряды треугольника. Потрясающе, правда? Называются эти отношения правилом Паскаля .

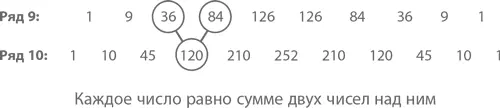
Почему так происходит? Когда мы смотрим на равенство 120 = 36 + 84, мы, по сути, видим

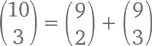
Чтобы в этом разобраться, давайте попробуем ответить на один вопрос. Если имеется 10 сортов мороженого, сколько вазочек можно собрать из 3 шариков разных сортов (порядок шариков при этом не важен)? С одной стороны, мы уже посчитали это количество как 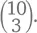Но есть и другой способ. Допустим, один из предлагаемых нам сортов мороженого – ванильное. Сколько вазочек у нас получится без него? Ответ – 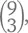потому что тогда мы будем выбирать свои 3 сорта из 9 оставшихся. А сколько вазочек получится с ним? Конечно же, 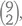ведь нам останется выбрать только 2 сорта из 9 оставшихся. Получается, что общее количество вазочек будет равно 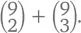Какой из этих ответов верен? И в том и в другом случае мы следовали абсолютно верной логике, поэтому и в том и в другом случае мы дали абсолютно верный ответ и получили абсолютно одинаковые результаты. Та же логика (или та же алгебра, если хотите) приводит нас к идее, что для каждого значения k от 0 до n

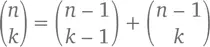
А теперь давайте посмотрим, что будет, если мы сложим все числа каждого ряда Паскалева треугольника (см. ниже).

Закономерность предполагает, что сумма всегда будет представлять собой степень двойки. Алгебраически: сумма чисел ряда n будет равна 2 n . Как так получается? Эту закономерность можно описать и по-другому: сумма чисел (числа) 1-го ряда равняется 1 и затем удваивается от ряда к ряду. Объяснением этому служит правило Паскаля, природу которого мы только что объяснили, а обоснованность – доказали. Например, когда мы складываем между собой числа 5-го ряда и трансформируем их в зависимости от их связи с 4-м рядом, получается