Артур Бенджамин - Магия математики: Как найти x и зачем это нужно
- Название:Магия математики: Как найти x и зачем это нужно
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2016
- Город:Москва
- ISBN:978-5-9614-4466-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Артур Бенджамин - Магия математики: Как найти x и зачем это нужно краткое содержание
«Магия математики» – та книга, о которой вы мечтали в школе. Все, от чего раньше голова шла кругом, теперь оказывается простым и ясным: треугольник Паскаля, математическая бесконечность, магические свойства чисел, последовательность Фибоначчи, золотое сечение. А ещё профессиональный фокусник Артур Бенджамин делится секретами математических фокусов. Продемонстрируйте их – ваши зрители точно потянутся за калькуляторами, чтобы пересчитать.
Магия математики: Как найти x и зачем это нужно - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
На n -ный день вы будете счастливым обладателем
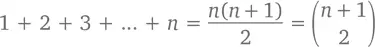
подарков (получилось это из нашей суперполезной формулы для треугольных чисел или из правила клюшки при k = 1). Так вот, первый день – 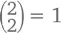 подарок, второй день –
подарок, второй день – 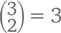 подарка и т. д., вплоть до 12-го дня, в который вы получите
подарка и т. д., вплоть до 12-го дня, в который вы получите 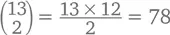 подарков. А правило хоккейной клюшки приводит нас к общему их количеству:
подарков. А правило хоккейной клюшки приводит нас к общему их количеству:

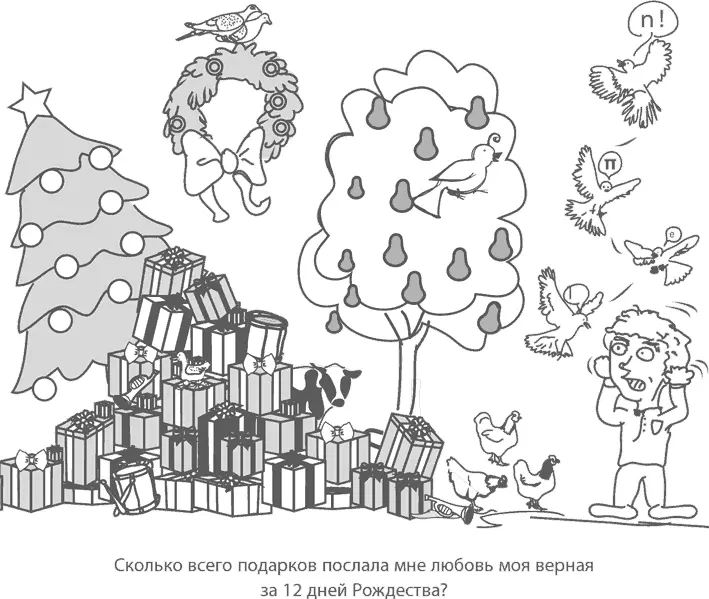
То есть если открывать по подарку каждый день – вам хватит их почти до конца года (ну, один можно пропустить в день рождения)!
Давайте теперь cпоем песенку, чтобы отпраздновать свой успех. Называется она « N -ный день Рождества».
В n -ный день Рождества послала мне любовь моя верная
n удивительных лакомств
n – 1 с одним вкусом,
n – 2 с другим; и остальных вкусностей
…
5 (плюс 10) всяких вкусностей!
А через n дней,
Усевшись считать подарки,
Сколько же я насчитал(а)?
Ровно 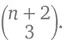
А вот одна из самых странных закономерностей Паскалева треугольника. На рисунке ниже отмечены все нечетные числа. Присмотритесь к ним и увидите в большом треугольнике несколько маленьких.

А теперь давайте сделаем вот что: сначала продлим большой треугольник до 16 рядов, а затем заменим все нечетные числа единицами, а все четные – нолями. Обратите внимание, что под каждой парой нолей, равно как и под каждой парой единиц, стоит ноль. Причина этого – в том, что при сложении 2 четных или 2 нечетных чисел сумма будет выражена четным числом.
Не будем на этом останавливаться: посмотрим на еще больший треугольник – из 256 рядов, – в котором все нечетные числа заменены черными квадратиками, а все четные – белыми.
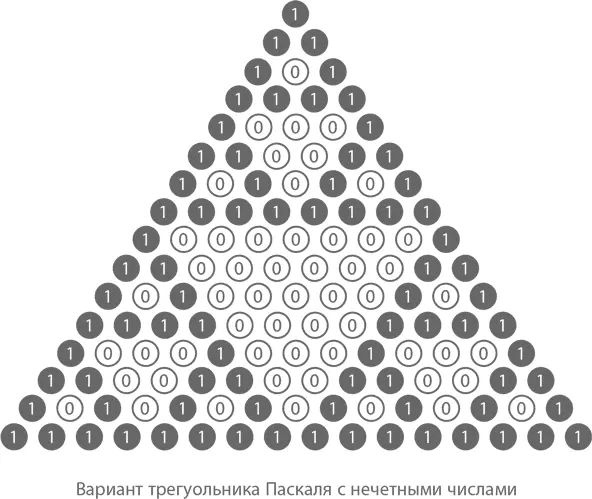

По сути своей данная фигура – это фрактал, или рекурсивное изображение, известное так же как треугольник Серпинского , – один из огромного количества сокровищ, скрытых в глубинах Паскалева клада. А вот еще один. Сколько всего нечетных чисел в каждом ряду треугольника Паскаля? Смотрим на ряды с 1 по 8 (без нулевого) и считаем: 2, 2, 4, 2, 4, 4, 8, 2 и т. д. Вроде бы никакой закономерности. Кроме того, что у нас всегда получается число, являющееся степенью 2. Это и есть та самая, нужная нам закономерность. Обратите внимание, что ряды, количество нечетных чисел в которых равно именно 2, – это 1, 2, 4 и 8-й. То есть обозначены они числами, которые сами являются степенью 2. Для более общего вывода нам нужно вспомнить, что любое целое число, которое больше 0 или равно ему, можно получить от сложения степеней числа 2 . Смотрите сами:
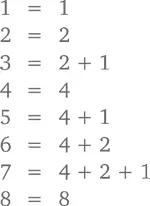
В рядах 1, 2, 4 и 8 (порядковые номера которых суть степени 2) у нас по 2 нечетных числа. В рядах 3, 5 и 6 (порядковые номера которых суть сумма двух степеней 2) у нас по 4 нечетных числа. В ряду же 7 (порядковый номер которого есть сумма трех степеней 2) – 8 нечетных чисел. Отсюда следует удивительное по своей красоте правило. Если n есть сумма p различных степеней числа 2, количество нечетных чисел в ряду n равняется 2 p. Сколько, например, нечетных чисел будет в 83-м ряду? Так как 83 = 64 + 16 + 2 + 1 (то есть сумма четырех степеней 2), наш ответ будет 2 4= 16!
Не будем на этом подробно останавливаться, но, если вам интересно, 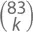 будет нечетным числом всякий раз, когда
будет нечетным числом всякий раз, когда
при a, b, c и d равных нолю или единице. Говоря точнее, k будет равно одному из этих чисел:
И под самый конец главы – еще одна закономерность. Мы уже видели, что происходит, если сложить числа в рядах (степень 2) и столбцах («хоккейная клюшка») Паскалева треугольника. А что будет, если сложить их по диагонали?
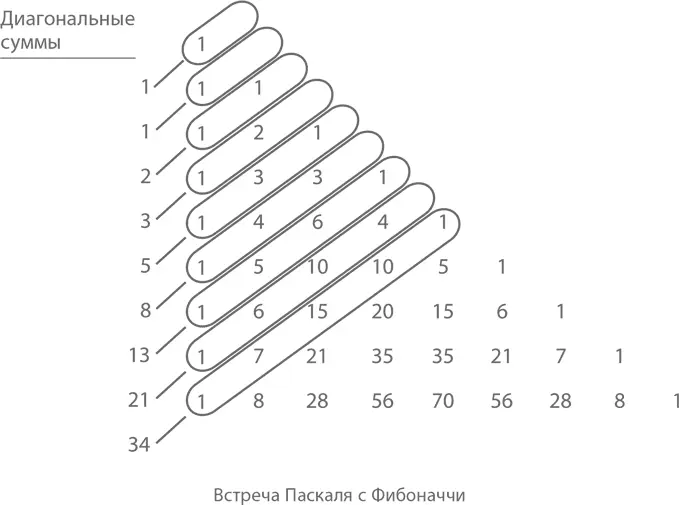
Смотрите, какие суммы выходят:
Не буду томить вас. Это числа знаменитой последовательности Фибоначчи, которая окажется в центре нашего внимания в следующей главе.
Глава номер пять
Магия последовательности Фибоначчи
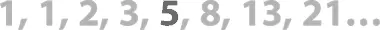
Числа матушки Природы
Лицезрите во всей красе одну из самых таинственных числовых последовательностей – последовательность Фибоначчи!
В ее начале находятся два одинаковых числа – 1 и 1. Третье число – это 1 + 1 (сумма двух предыдущих чисел), то есть 2. Четвертое – 1 + 2 = 3, пятое – 2 + 3 = 5 и т. д. и т. п. Очень похоже на чехарду: 3 + 5 = 8; 5 + 8 = 13; 8 + 13 = 21… Впервые эти числа в таком виде появились в книге 1202 года Liber Abaci («Книга абака», в буквальном переводе с латинского – «Книга вычислений») за авторством Леонардо Пизанского, впоследствии прозванного Фибоначчи. Значение этого труда для европейской цивилизации переоценить невозможно: он впервые знакомил западного читателя с индо-арабскими цифрами и ставшими уже привычными для нас арифметическими методами.
Одна из самых известных включенных в него задач – задача о бессмертных кроликах. Допустим, крольчонку требуется месяц, чтобы повзрослеть. От каждой пары кроликов каждый месяц рождается еще пара – и так до бесконечности, поскольку наши кролики бессмертны. Вопрос: если начать с одной пары, сколько у нас будет пар кроликов 12 месяцев спустя?
Читать дальшеИнтервал:
Закладка:









