Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

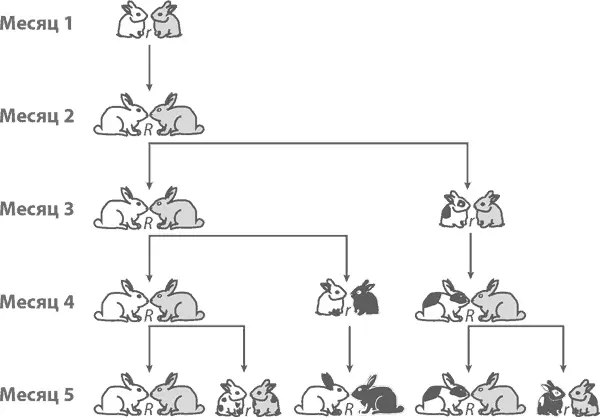
Иллюстрировать задачу можно либо картинкой, либо таблицей. Маленькой буквой r отметим пары малюток-крольчат, большой R – пары взрослых кроликов. От месяца к месяцу каждая маленькая r становится большой R , а каждая большая R заменяется R и r (это означает, что крольчата вырастают, а затем от них рождается пара новых крольчат).

Всю эту ситуацию мы можем представить в виде таблицы. Здесь хорошо видно, что в первые 6 месяцев число пар кроликов равняется соответственно 1, 1, 2, 3, 5 и 8.

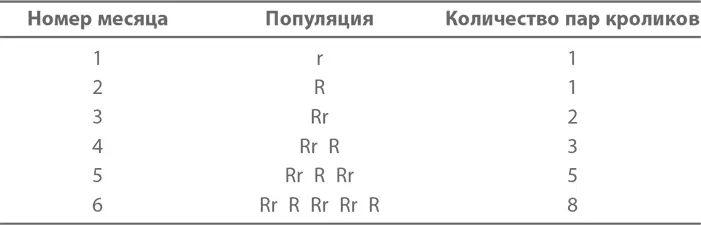
Давайте попробуем доказать, что на седьмой месяц у нас будет уже 13 пар, ничего при этом не рисуя и не фиксируя на листочке. Сколько к этому моменту будет пар взрослых кроликов? Так как каждая пара из тех, что получились у нас к шестому месяцу, к седьмому успела повзрослеть, получаем 8 пар.

А сколько будет пар крольчат? Их число будет равняться числу пар взрослых кроликов шестого месяца (то есть 5) или общему количеству пар пятого месяца (и такое совпадение совсем не случайно). Следовательно, на седьмой месяц у нас будет 8 + 5 = 13 пар.

Если мы назовем первые два числа последовательности Фибоначчи F 1= 1 и F 2= 1, а потом определим каждое следующее число как сумму предшествующих ему двух, то, при n ≥ 3 получим

И тогда F 3= 2, F 4= 3, F 5= 5, F 6= 8 и т. д. по таблице:

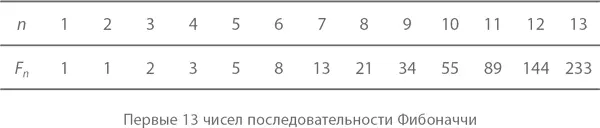
Следовательно, ответом на задачу Фибоначчи о бессмертных кроликах будет F 13= 233 пар, из которых F 12= 144 будут взрослыми, а F 11= 89 – крольчатами.

Эта последовательность пригодна не только для подсчета численности популяций животных. Числа Фибоначчи встречаются даже в самой природе, и на удивление часто: это и лепестки цветка, и спирали подсолнуха, ананаса или сосновой шишки. Меня в последовательности Фибоначчи больше всего восхищают обнаруживающиеся в ней замечательные числовые закономерности.

Давайте для начала сложим несколько первых из этих чисел:

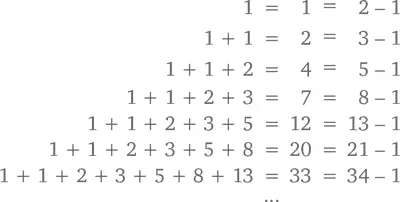
Числа справа к последовательности не относятся, но находятся совсем рядом с ней – буквально в одном шаге. Давайте разберемся, что тут происходит. Возьмем последнее из этих уравнений и посмотрим, что произойдет, если заменить каждое из чисел Фибоначчи на разность двух следующих после него. То есть

Обратите внимание, как двойка из (2 – 1) перекрывается двойкой из (3 – 2), а тройка из (3 – 2) перекрывается тройкой из (5 – 3). Собственно говоря, перекрываются здесь практически все числа, за исключением самого большого 34 и начального –1. Означает это, что сумма первых n чисел последовательности Фибоначчи вычисляется по формуле

А вот еще один вопрос, напрямую связанный с первым и имеющий не менее элегантный ответ. Что мы получим, если захотим сложить между собой первые n чисел, занимающих четные позиции в последовательности? Другими словами, получится ли у нас упростить сумму

Давайте сначала посмотрим на некоторые из них:

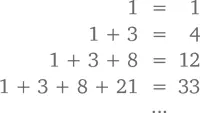
Погодите-ка. Вроде бы что-то знакомое. Мы же уже видели эти числа, когда считали прошлую сумму. Они на единицу меньше чисел Фибоначчи. По сути, каждое из них может быть трансформировано подобным образом на том основании, что каждое из чисел Фибоначчи – сумма двух предыдущих. Именно этой суммой мы можем заменить каждое число, занимающее четную позицию в последовательности, вот так:

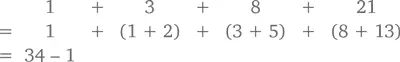
Последняя строчка получается благодаря тому, что сумма первых 7 чисел последовательности лишь на единицу меньше девятого.

В целом, если мы будем исходить из того, что F 2= F 1= 1, и заменять каждое последующее число суммой двух предыдущих, мы увидим, что нужную нам сумму можно легко свести к сумме первых 2 n – 1 чисел последовательности.

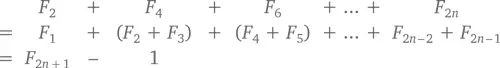
А теперь давайте посчитаем сумму первых n чисел, занимающих нечетные позиции.

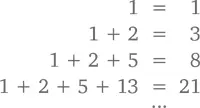
Здесь все еще проще, как ни странно. Сумма n чисел, занимающих нечетные позиции в последовательности, – это просто следующее число Фибоначчи. Представить это можно следующим образом:

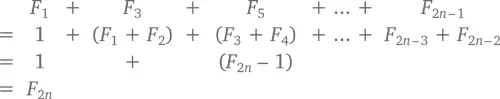
К ответу можно прийти и другим способом – с помощью того, о чем мы только что говорили. Если мы вычтем первые n чисел, стоящих в последовательности на четных позициях, из первых 2 n чисел, получатся первые n чисел, находящиеся на нечетных позициях:

Мы заглянули лишь в замочную скважину той двери, за которой раскинулся сад самых настоящих чудес. Только растут в нем не деревья, а числовые закономерности, уходящие корнями в последовательность Фибоначчи. И вам, наверняка, не терпится узнать, для чего еще, кроме подсчета поголовья кроликов, нужны эти числа. На самом деле – много для чего. В 1150 году (задолго до того, как Леонардо Пизанский представил миру задачку про кроликов) индийский поэт Хемачандра задался очень интересным вопросом: сколькими способами можно сложить стихотворную стопу из n безударных или ударных слогов. Давайте сперва переведем эту проблему из плоскости поэзии в плоскость математики.