Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

На занятиях по геометрии в школе или университете очень много внимания уделяется доказательству конгруэнтности объектов: это значит, что, перемещая, вращая или отображая зеркально одну фигуру, мы можем получить совпадающую с ней другую. Например, изображенные на рисунке треугольники ABC и DEF являются конгруэнтными, поскольку при смещении влево треугольник DEF полностью совпадет с треугольником ABC . На рисунке это показано с помощью специальных меток: если соответствующие стороны или углы двух фигур маркированы одинаковым количеством черточек, они равны.

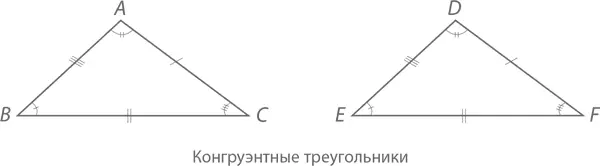
Для этого даже есть специальный математический символ – ≅; наша запись, таким образом, будет выглядеть как ABC ≅ DEF , что значит, что стороны обоих треугольников и их углы идеально друг с другом совпадают: стороны AB, BC и CA равны сторонам DE, EF и FD (соответственно), а углы по вершинам A, B и C равны углам по вершинам D, E и F (также соответственно). Именно это мы и имеем в виду, когда отмечаем одинаковым количеством черточек совпадающие стороны и углы этих двух по сути разных (хоть и равных) треугольников.

Остальное – дело техники. Если вы, например, имеете дело с двумя равносторонними треугольниками и знаете, что углы двух из трех пар равны (допустим, ∠ A = ∠ D и ∠ B = ∠ E ), вы можете смело утверждать, что равными будут углы и третьей пары – а значит, треугольники являются конгруэнтными. Информации тут даже больше, чем нужно: нам вполне достаточно знать, что равными будут боковые стороны треугольников ( AB = DE и AC = DF ) и углы между ними (∠ A = ∠ D ). А дальше все просто: BC = EF , ∠ B = ∠ E , а ∠ C = ∠ F . Из этого вытекает аксиома конгруэнтности треугольников по двум сторонам и лежащему между ними углу .

Это именно аксиома, а не теорема, поскольку доказать ее с помощью уже существующих аксиом невозможно. Зато, принятая на веру, она ложится в основу других не менее полезных теорем конгруэнтности а) по трем сторонам; б) по одной стороне и двум прилежащим к ней углам; и в) по двум углам и прилежащей к одному из них стороне. (Не существует только теоремы конгруэнтности по двум сторонам и прилежащему к одной из них углу: для стопроцентной уверенности угол все же должен находиться между сторонами.) Самой интересной из них мне кажется теорема а), ведь изначально в ней вообще никак не упоминаются углы, равенство которых доказывается через равенство сторон.

Но вернемся к аксиоме по двум сторонам и углу между ними и докажем с ее помощью одну замечательную теорему, касающуюся равнобедренных треугольников. Равнобедренным называется такой треугольник, две из трех сторон которого имеют одинаковую длину. (И кстати, уж коли об этом зашла речь – есть и другие виды треугольников: равносторонние – в которых все три стороны равны; прямоугольные – в которых один угол равен 90°; остроугольные – в которых все три угла меньше 90°; и, наконец, тупоугольные – в которых один угол больше 90°.)

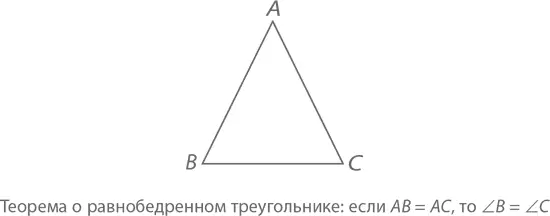
Теорема о равнобедренном треугольнике:Если в равнобедренном треугольнике ABC стороны AB и AC равны, противолежащие этим сторонам углы будут также равны.

Доказательство:Из точки A проведем линию так, чтобы она делила ∠ A ровно пополам и пересекала отрезок BC в точке X , как на рисунке. Это биссектриса угла A .

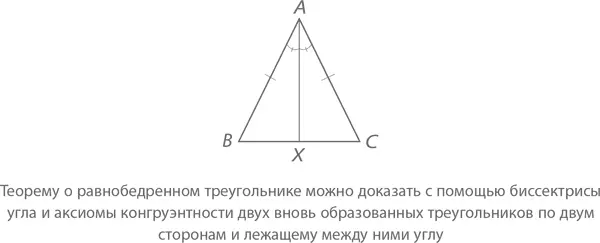
Получившиеся таким образом треугольники BAX и CAX являются конгруэнтными согласно аксиоме по двум сторонам и лежащему между ними углу: BA = CA (что следует из понятия равнобедренности), ∠ BAX = ∠ CAX (что следует из понятия биссектрисы), а AX = AX (вернее, не так: отрезок AX не уникален, он появляется одновременно в двух треугольниках и не меняет свою длину). А так как BAX ≅ CAX, также равны будут и остальные стороны и углы, в том числе ∠B = ∠C, что и требовалось доказать.◻

То же можно доказать и с помощью теоремы конгруэнтности по трем сторонам. Для этого возьмем точку M как середину отрезка BC , то есть чтобы BM было равно MC . Проведем линию по отрезку AM . Как и в предыдущем доказательстве, треугольники BAM и CAM будут конгруэнтными, потому что BA = CA (равнобедренность), AM = AM , а MB = MC (потому что точка M находится ровно посередине BC ). Следовательно, согласно доказательству по трем парам сторон, BAM ≅ CAM , что говорит нам о равности лежащих в них углов, в том числе и ∠ B = ∠ C , что и требовалось доказать.

Из факта конгруэнтности следует, что ∠ BAM = ∠ CAM , следовательно, отрезок AM является биссектрисой. Более того, так как ∠ BMA = ∠ CMA и в сумме они дают 180°, каждый из них должен быть равен 90°, из чего следует вывод, что в равнобедренном треугольнике биссектриса, проложенная из угла A , будет перпендикуляром к основанию BC .

Кстати, доказательство от обратного в отношении равнобедренного треугольника тоже вполне эффективно, то есть если ∠ B = ∠ C , то AB = AC . Для этого, как и в самом первом доказательстве, проведем биссектрису из точки A в точку X . Утверждение, что BAX ≅ CAX , в этом случае следует из теоремы конгруэнтности по двум углам и прилежащей к одному из них стороне: ∠ B = ∠ C (согласно изначальному условию), ∠ BAX = ∠ CAX (согласно определению биссектрисы), а AX = AX . Значит, AB = AC , то есть треугольник ABC является равнобедренным.

Теорему эту можно применить и к равностороннему треугольнику: если равны все стороны, значит, равны и все углы. Следовательно, поскольку в сумме своей три угла дают 180°, имеем сопутствующую теорему.

Сопутствующая теорема:В равностороннем треугольнике каждый из углов равен 60°.

Согласно теореме конгруэнтности по трем сторонам, если в треугольниках ABC и DEF совпадают все стороны (то есть AB = DE, BC = EF , а CA = FD ), их углы будут также совпадать (то есть ∠ A = ∠ D , ∠ B = ∠ E , а ∠ C = ∠ F ). Верным ли будет обратное предположение, что, если в треугольниках ABC и DEF совпадают все углы, будут совпадать и их стороны? Конечно же, нет – просто посмотрите на рисунок: