Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

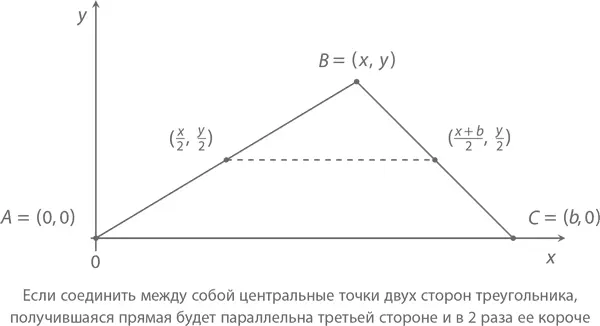
Теорема о центральных точках треугольника поможет нам разгадать фокус, с которого начиналась эта глава: тогда мы взяли четырехугольник ABCD и соединили центральные точки его сторон так, что образовался еще один четырехугольник, EFGH , который оказался (и всегда окажется) параллелограммом. Давайте разберемся, почему так происходит. Диагональная линия, проведенная от вершины A к вершине C , образует два треугольника ABC и ADC (см. рисунок).

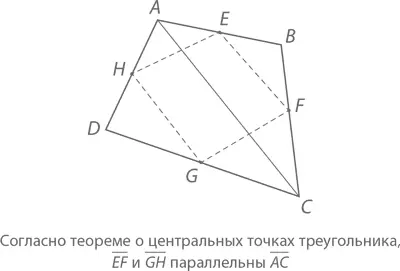
Применив теорему о центральных точках треугольника, мы обнаружим, что отрезок EF будет параллелен отрезку AC , который в свою очередь будет параллелен отрезку GH . Следовательно, EF будет параллельна GH . (Более того, EF и GH будут иметь одинаковую длину, равную половине AC .)

Проведем точно такую же диагональ из вершины B к вершине D и увидим, что FG и HE также параллельны и равны по длине. Следовательно, EFGH является параллелограммом.

Большинство из разобранных нами теорем связано с треугольниками, что ничуть не удивительно, ведь в геометрии этой фигуре уделяется много внимания. Кстати сказать, треугольник есть не что иное, как наипростейшая разновидность полигонов (многоугольников). Дальше идут четырехугольник (четырехсторонний полигон), пятиугольник (пятисторонний полигон) и так далее. Полигон, количество сторон которого равно n , иногда называется n -угольником. Мы уже доказывали, что сумма всех углов треугольника равна 180°. А что насчет остальных полигонов? Любой четырехугольник, будь то квадрат, прямоугольник или параллелограмм, имеет четыре стороны. В прямоугольнике, как явствует из его названия, все 4 угла являются прямыми, то есть равными 90°, а значит, составляют в сумме 360°.

Следующая наша теорема будет верна для любого четырехугольника.

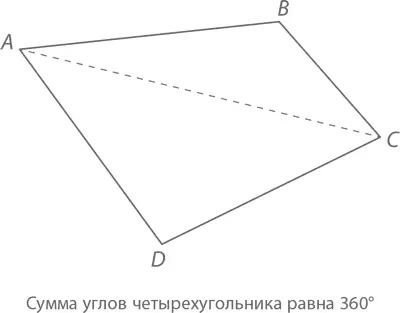
Теорема:Сумма углов четырехугольника равна 360°.

Доказательство:Возьмем любой четырехугольник с вершинами A, B, C и D (вроде того, что изображен на рисунке). Из угла A в угол C проведем линию так, чтобы она разделила четырехугольник на 2 треугольника, сумма углов каждого из которых равна 180°. Следовательно, сумма углов четырехугольника составит 2 × 180° = 360°

Чтобы проследить общую закономерность, разберем еще одну теорему.

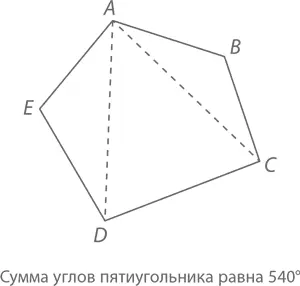
Теорема:Сумма углов пятиугольника равна 540°.

Доказательство:Возьмем пятиугольник с вершинами A, B, C, D и E (вроде того, что изображен на рисунке). Линия, проведенная от вершины A к вершине C , разделит пятиугольник на четырех– и треугольник. Сумма углов треугольника ABC составляет 180° (это мы знаем уже давно), сумма углов четырехугольника ACDE – 360° (это мы доказали только что). Следовательно, сумма углов пятиугольника – 180° + 360° = 540°.

Этот алгоритм можно применять снова и снова, к любому полигону, вплоть до n -угольника.

Здесь отлично сработает метод индукции: для этого надо разделить наш n -угольник на n – 2 треугольников, поэтапно соединяя линиями вершину A со всеми остальными.

Теорема:сумма углов n-угольника равна 180( n – 2) градусам.

А теперь… просто следите за волшебной палочкой! Начертите восьмиугольник (восьмисторонний полигон) и поставьте внутри него 5 точек – где угодно. А теперь соедините их с вершинами углов и друг с другом так, чтобы у вас получались треугольники (именно треугольники – никаких других фигур). Процесс этот называется триангуляцией, и вот несколько его примеров. (Последний восьмиугольник я оставил пустым, чтобы вы могли проделать это сами.)

В обоих моих примерах восьмиугольники разбиты ровно на 16 треугольников. Столько же должно получиться у вас в третьем октагоне вне зависимости от того, где именно вы поставили 5 точек. (А если вдруг нет, значит, вы где-то ошиблись – в этом случае просто внимательно приглядитесь к каждой доле и убедитесь, что в ней ровно 3 точки, а не 4; если же их все-таки 4, проведите линию от одного угла доли к другому, чтобы разделить ее на два треугольника.) Объяснить это можно с помощью следующей теоремы.

Теорема:В процессе триангуляции n -сторонний полигон, имеющий внутри некое количество точек, равное p , будет разделен ровно на 2 p + n – 2 треугольников.

В нашем предыдущем примере n = 8, а p = 5, поэтому треугольников получается 10 + 8 – 2 = 16.

Доказательство:Предположим, что в процессе триангуляции у нас получается количество треугольников, равное T . Мы можем доказать, что T = 2 p + n – 2, решив одну арифметическую задачку двумя разными способами. Итак, внимание!

Вопрос: Чему будет равна сумма углов всех треугольников?

Ответ 1: Так как количество треугольников равно T , а сумма углов каждого из них – 180°, общая сумма составит 180 T градусов.

Ответ 2: Разобьем задачу на две. Углы, прилежащие к каждой из внутренних точек (напомним, что их количество равно p ), образуют окружность, следовательно, их общая сумма составит 360 p градусов. С другой стороны, из предыдущей теоремы мы знаем, что сумма углов n -угольника равна 180( n – 2) градусам. Значит, всего получится 360 p + 180( n – 2) градусов.

Из двух ответов составим уравнение

Разделим обе части на 180, что даст нам

что и требовалось доказать.☺

Периметр полигона есть сумма длин его сторон. Так, периметр прямоугольника длиной b и шириной h будет равен 2 b + 2 h , потому что и b , и h суть размеры каждой из двух его сторон. А как насчет площади? Исходим из того соображения, что площадь квадрата размером 1 на 1 (так называемого единичного квадрата) равна 1. При положительных целых значениях b и h (как на рисунке) мы можем разбить всю площадь на bh единичных квадратов, а значит, она будет равна bh . В целом же, любой прямоугольник с длиной b и шириной h (где b и h суть положительные, но необязательно целые величины) имеет площадь bh .