Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Если же мы разложим 32 на 4 и 8, получим 38 × 4 × 8 = 152 × 8 = 1216, но я лично предпочитаю умножать двузначное число сначала на больший сомножитель, а промежуточный результат (обычно трехзначный) – на меньший.

Метод разложения отлично работает при умножении на 11 – хотя бы потому, что здесь есть один любопытный и при этом простой трюк: нужно просто сложить между собой цифры первого числа и поместить сумму в его середину. Для примера умножим 53 на 11: 5 + 3 = 8, значит, ответ будет 583. А вот 27 × 11 ÷ 2 + 7 = 9, в итоге получаем 297. А если сумма больше 9, берем последнюю цифру результата сложения, а первую цифру исходного числа увеличиваем на единицу. Например, 48 × 11 ÷ 4 + 8 = 12, значит, ответ будет 528. По аналогии: 74 × 11 = 814. Этот трюк работает и при умножении на числа, кратные 11, например,

Другой интересный метод – метод сближения . Его можно использовать, когда двузначные числа , которые вы перемножаете, начинаются с одной и той же цифры . Неискушенному наблюдателю он может показаться настоящим фокусом. Ведь разве можно просто взять и поверить, что

Вычисления становятся элементарными, если последние цифры двух чисел дают в сумме 10 (как в нашем примере: оба числа начинаются с 3, а сумма их последних цифр – 8 и 2 – равна 10). Вот еще один пример:

Но даже если вторые цифры не дадут в сумме 10, метод от этого не станет менее эффективным и эффектным, да и вычисления усложнятся не так уж и сильно. Чтобы умножить, например, 41 на 44, сначала надо уменьшить меньшее из них на единицу (чтобы работать с круглым числом 40) и, соответственно, увеличить на ту же единицу большее число:

Для 34 × 37 отнимаем 4 у 34 (и остается 30) и отдаем их 37 (37 + 4 = 41), а потом прибавляем 4 × 7:

Кстати, помните загадочный пример с 104 × 109? Там использовался тот же самый метод:

В некоторых школах, кстати, учеников заставляют учить не привычную таблицу умножения, которая заканчивается 10, но расширенную до 20. Наш метод сводит эту необходимость на нет:

Как же так получается, что эта штука работает, спросите вы? Чтобы разобраться, нужно обратиться к алгебре – этим мы займемся в главе 2. А алгебра даст нам еще больше способов счета. Например, ту же задачу можно будет решить еще и вот так:

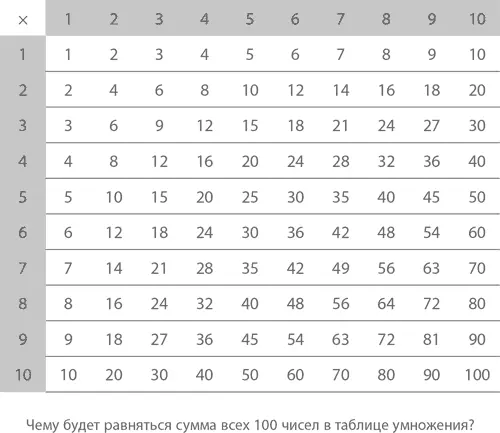
Кстати, о таблице умножения: взгляните на столбцы и ряды однозначных чисел чуть ниже (я же обещал вам это показать, помните?). Перед нами встанет тот же вопрос, который встал перед юным Гауссом: чему будет равняться сумма всех чисел таблицы умножения? Не торопитесь, подумайте: вдруг у вас получится найти ответ каким-нибудь волшебным, потрясающим воображение способом? Ну а свой способ я предложу вам в конце главы.

Давайте начнем с очень простого вопроса, на который существует очень простой ответ, которому по какой-то неизвестной причине не учат в школах:

а) если вам нужно перемножить два трехзначных числа, сможете ли вы сразу сказать, из скольки знаков будет состоять результат?

И чуть посложнее:

б) число из скольки знаков получится, если умножить четырехзначное число на пятизначное?

В школе почти все время уходит на то, чтобы подбирать цифры при умножении и делении, а не на то, чтобы подумать о том, насколько большим будет результат. Да-да, умение примерно оценивать, насколько большим будет ответ, куда важнее умения находить его последние или даже первые цифры. (Подумайте сами, какой практический прок от знания того, что итог начинается с цифры 3, и не полезнее ли знать, к чему он будет ближе: к 30 или 300 000 или вовсе к 3 000 000?)

Ответ на вопрос (а) – из пяти или шести цифр. Знаете почему? Минимальный возможный пример – 100 × 100 = 10 000 (здесь пять цифр). Максимальный – 999 × 999, результат которого однозначно будет меньше семизначного 1000 × 1000 = 1 000 000 (пусть и ненамного). Но раз 999 × 999 меньше, значит, в ответе будет шесть цифр (давайте, кстати, вспомним, насколько легко это посчитать: 9992 = (1000 × 998) + 12 = 998 001.) Вот и вывод: результатом перемножения двух трехзначных чисел будет пяти– или шестизначное число.

Ответ на вопрос (б) – из восьми или девяти цифр. Почему? Наименьшее четырехзначное число – 1000, которое можно представить в виде 10³ (единица с тремя нолями). Наименьшее пятизначное число – 10 000, равное 10 4. Следовательно, наименьшим произведением 10³ и 10 4будет 10 7 – единица с семью нолями, восьмизначное число. (Откуда взялось 10 7? Смотрите: 10³ × 10 4= (10 × 10 × 10) × (10 × 10 × 10 × 10) = 10 7.) Ну а наименьшим произведением будет число, лишь ненамного меньшее десятизначного 10 4× 10 5= 10 9, то есть девятизначное.

Такая логика приводит нас к простому правилу: умножение m -значного числа на n -значное даст число, в котором m + n или m + n – 1 знаков.

Конкретное количество цифр в ответе легче всего определить, взглянув на начальные (крайние левые) цифры перемножаемых чисел. Если их произведение больше или равно 10, тогда в ответе будет m + n цифр (например, в 271 × 828 произведение крайних левых цифр – 2 × 8 = 16 – больше десятки, поэтому ответом будет шестизначное число). Если произведение крайних левых цифр меньше или равно 4, тогда в ответе будет m + n – 1 цифр (например, 314 × 159 будет иметь пятизначный ответ). Ну а на случаи, в которых произведение крайних левых цифр будет равняться 5, 6, 7, 8 или 9, нам придется посмотреть чуть более внимательно. Например, произведение 222 и 444 – пятизначное, а вот 234 и 456 – шестизначное. Но куда важнее то, что оба ответа очень близки к 100 000.

В результате у нас получается еще более простое правило, уже в отношении деления: деление m -значного числа на n -значное даст число, в котором m – n или m – n + 1 знаков.

То есть девятизначное число, разделенное на пятизначное, даст нам четырех– или пятизначный результат. Правило определения более конкретного ответа здесь еще проще, чем в случае с умножением. Крайние левые цифры не нужно ни умножать, ни делить – достаточно их просто сравнить . Если крайняя левая цифра делимого меньше крайней левой цифры делителя, в частном будет меньшее количество цифр ( m – n ). Если же крайняя левая цифра делимого больше крайней левой цифры делителя, в частном будет больше ( m – n + 1) цифр. Если же цифры обоих чисел одинаковые, смотрим на следующие после них цифры и применяем то же правило. Например, в результате деления 314 159 265 на 12 358 мы получим пятизначное число, а на 62 831 – четырехзначное. Деление 161 803 398 на 14 142 даст пятизначный ответ, потому что 16 больше 14.