Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Рассказывать в подробностях про процесс деления в уме я здесь не буду: он мало чем отличается от деления в столбик на бумаге (но каким бы методом вы ни воспользовались, считать нужно слева направо). Но есть парочка уловок, которые значительно облегчат вам жизнь.

Скажем, если вы делите на 5 (или на любое число, заканчивающееся на 5), удвойте числитель и знаменатель, и задача станет проще. Например,

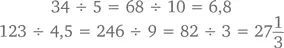
После удвоения обоих чисел хорошо видно, что и 246, и 9 кратны 3 (мы поговорим об этом подробнее в главе 3), поэтому задача упрощается до деления отдельно числителя и знаменателя на 3.

Взгляните на взаимно обратные числа для чисел от 1 до 10:

Все дроби здесь либо конечны, либо цифры в них начинают повторяться со второго знака после запятой. Единственным исключением является десятичная дробь от 1/7, повторение в которой начинается с седьмой цифры:

(Причина этой закономерности в том, что все другие числа от 2 до 11 делятся на 10, 100, 1000, 9, 90 или 99, ближайший же делитель для 7 – 999 999.) Если же записать цифры десятичного аналога 1/7 в виде круга, произойдет чудо:

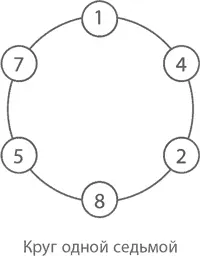
Что интересно, все другие дроби со знаменателем 1/7 тоже могут воссозданы с помощью бесконечного движения по этому кругу – меняться будет только точка начала этого движения. Посмотрите сами:

Давайте закончим эту главу тем же вопросом, который мы уже задавали несколько страниц назад. Чему будет равняться сумма всех чисел в таблице умножения? На первый взгляд звучит пугающе – так же, как и попытка найти сумму первых ста чисел. Но знакомство со всеми описанными выше замечательными закономерностями, которые так ловко заставляют числа танцевать, значительно повышают наши шансы легко и красиво найти правильный ответ.

Начнем с первого ряда – посчитаем сумму всех чисел в нем. Можно – как Гаусс, можно – с помощью формулы треугольных чисел, а можно – путем обычного сложения:

Так, теперь второй ряд. Вот как это будет выглядеть:

По той же логике, 3 ряд будет равен 3 × 55. И так далее, и тому подобное, и в результате сумму всех чисел в таблице умножения можно подсчитать так:

Ну а возвести в уме 55 в квадрат вы теперь можете легко и просто… 3025!

Первый раз я столкнулся с алгеброй еще в детстве – мой отец вдруг решил дать мне урок вычислений:

– Сын, – сказал он мне. – Алгебра – все равно что арифметика. За тем исключением, что вместо чисел ты пишешь буквы. Вот, смотри: 2 х + 3 х = 5 х , а 3 у + 6 у = 9 у . Понимаешь?

– Вроде, понимаю.

– Очень хорошо, – сказал он. – А сколько тогда будет 3β + 4β?

– 7β, – уверенно ответил я.

– Что-то я тебя не слышу, – посетовал папа. – Можешь погромче?

– СЕМЬБЕТА!!! – заорал я.

– И ни одного ответа! – с готовностью отозвался папа. Он всегда предпочитал каламбуры, шутки и забавные истории скучным вычислениям, так что такой исход я мог бы и предвидеть.

Второй раз алгебра улыбнулась мне, когда я пытался понять один магический трюк – сейчас расскажу, какой.

Шаг 1. Задумайте число от 1 до 10 (хотя, по большому счету, можно и большее).

Шаг 2. Умножьте это число на 2.

Шаг 3. Добавьте 10.

Шаг 4. Разделите на 2.

Шаг 5. Вычтите из результата изначально задуманное вами число.

Уверен, получилось 5. Правильно?

Хотите узнать, в чем кроется секрет волшебства? В алгебре. Разберем фокус еще раз, шаг за шагом, начиная с первого. Я понятия не имею, какое число вы загадали, поэтому давайте заменим его буквой N . Неизвестное число, обозначаемое буквой, называется переменной .

Шаг второй предлагает нам удвоить загаданное число, то есть мы, по сути, имеем 2 N (знак умножения в алгебре принято опускать, в том числе и потому, что очень часто для обозначения переменной используется внешне похожая на него буква x ). После третьего шага ваше число выглядит как 2 N + 10. Четвертая операция предлагает нам упростить пример, разделив все его части на 2: N + 5. И, наконец, мы вычитаем загаданное число (то есть N ): N + 5 – N = 5. Давайте соберем весь фокус в одну таблицу:

Начнем с загадки. Найдите число, которое становится в три раза больше, если к нему прибавить 5.

Чтобы ее решить, заменим неизвестное нам число буквой х . Добавление пятерки дает нам х + 5, утроение – 3 х . Мы хотим, чтобы эти две записи были равными, поэтому нам придется решать уравнение

Уберем по одному х из обеих его частей и получим

(смотрите, откуда берется 2 x : 3 x – x – то же, что и 3 x – 1 x , то есть 2 x ). Разделим обе части уравнения на 2:

Можем проверить правильность ответа: 2,5 + 5 = 7,5, Тот же ответ получаем, умножая 2,5 на 3.

А вот еще один фокус, в сути которого можно легко разобраться с помощью алгебры. Запишите любое трехзначное число, цифры в котором идут по убывающей (например, 842 или 951). Затем запишите эти числа в обратном порядке и вычтите второе число из первого. Какой бы ответ у вас ни получился, запишите в обратном порядке и его, а затем сложите эти два числа. Вот пример с числом 853:

Попробуйте другое число. Что вышло? А то, что, если четко и правильно выполнять все инструкции, вы всегда будете получать 1089! Как так?

Алгебра, помоги! Итак, начинаем мы с трехзначного числа abc , в котором a > b > c . Точно так же, как и 853 = (8 × 100) + (5 × 10) + 3, число abc равняется 100 a + 10 b + c . Записав его справа налево, получим число cba , равное 100 c + 10 b + a . Вычитание дает нам