Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Одним из самых важных и полезных следствий из закона дистрибутивности является алгебраическое правило FOIL [3], согласно которому для любых переменных a, b, c, d верно следующее:

Смотрите, как правило FOIL работает на практике: cначала мы перемножаем первые числа в ( a + b )( c + d ), то есть ac. Потом – внешние , то есть ad . Затем – внутренние: bc . И наконец – последние: bd .

Давайте проиллюстрируем все это примером с конкретными числами:

Почему работает правило FOIL? Согласно закону дистрибутивности (по отношению к части со сложением, идущей на первом месте),

А теперь вместо e подставим c + d , что даст нам

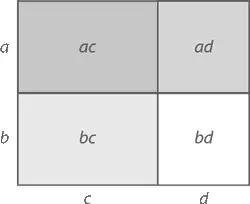
Последняя часть становится возможной благодаря повторному применению закона дистрибутивности. Если вы предпочитаете геометрически визуализированное доказательство (при условии, что a, b, c, d – положительные величины), то вот вам прямоугольник, площадь которого можно найти двумя различными способами.

С одной стороны, площадь можно высчитать с помощью ( a + b )( c + d ). С другой – мы можем разбить большой прямоугольник на четыре с площадями ac, ad, bc и bd . Значит, общая площадь будет равна ac + ad + bc + bd . Знак равенства между двумя этими подходами обеспечивает правило FOIL .

А теперь давайте посмотрим, как работает магия правила FOIL . Бросьте две игральные кости и посмотрите таблицу, которая приведена чуть ниже. Допустим, вы выкинули 6 и 3. На обратных сторонах костей будет, соответственно, 1 и 4.

В нашем примере результат будет равен 49. И сколько бы вы ни бросали обычные шестигранные кости, результат будет тот же. Дело в том, что сумма чисел на противоположных сторонах стандартной игральной кости всегда равна 7. То есть если обозначить выпавшие числа буквами x и y , их парами будут 7 – x и 7 – y . Алгебра переделывает нашу таблицу таким вот образом:

Обратите внимание на подсчет в третьей строке (– x и – y при умножении дают xy со знаком плюс). К результату 49 можно прийти и другим, менее алгебраическим, способом: достаточно просто посмотреть на второй столбец таблицы и увидеть там те самые четыре числа, которые нужны нам для «запуска» FOIL: ( x + (7 – x ))( y + (7 – y )) = 7 × 7 = 49.

На уроках алгебры правило FOIL обычно применяют для решения таких, например, задач:

В крайней правой части число 7 (которое в этом случае называется коэффициентом числа х ) есть сумма 3 и 4; 12 же (здесь он будет постоянным членом ) – их произведение. Ну а получить ответ с нашим-то опытом – дело элементарное: так как 5 + 7 = 12, а 5 × 7 = 35, получаем

С отрицательными величинами это тоже отлично работает, и вот тому подтверждение: в нашем первом примере мы начинаем с того, что 6 + (–2) = 4, а 6 × (–2) = –12.

А вот примеры, когда известные числа у нас одинаковые:

Обратите внимание, кстати, что ( x + 5)² ≠ x ² + 25: ошибку эту делают почти все, кто только начинает познавать азы алгебры. Но куда интереснее обстоят дела, когда у нас есть два одинаковых числа с разными знаками. Например, так как 5 + (–5) = 0,

Главное, что нужно запомнить – формула разности квадратов двух переменных :

Мы уже пользовались ей в главе 1, в примере, когда учились в уме возводить в квадрат числа. Способ этот основан на алгебраической формуле:

Сначала давайте удостоверимся в правильности этой формулы. В отличие от формулы квадратов здесь мы имеем [( A + d )( A – d )] + d ² = [ A ² – d ²] + d ² = A ². Стало быть, это действительно для всего диапазона значений A и d . На практике буквой A обозначается число, возводимое в квадрат, а d – его разность с ближайшим круглым числом. Например, чтобы возвести в квадрат 97, мы принимаем d за 3, чтобы получить

А вот несколько рисунков, доказывающих закон квадратичной зависимости. На них показано, как геометрическая фигура с площадью x ² – y ² может быть преобразована в прямоугольник с площадью ( x + y )( x – y ).