Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

что и является ответом (не забудьте проверить).

Применяя метод FOIL, получаем ( x + a )( x + b ) = x ² + ( a + b ) x + ab . Что превращает разложение на множители в непростую, в общем-то, задачку. Например, в последнем примере нам нужно найти два числа: a и b – с суммой 4 и произведением –12. Ответ – a = 6, b = –2 – позволяет нам достичь желаемого и разложить на множители. Давайте попрактикуемся и используем метод разложения на множители x ² + 11 x + 24. Другими словами, перед нами стоит задача найти два числа, которые в сумме давали бы 11, а при умножении – 24. Подходят 3 и 8, а значит x ² + 11 x + 24 = ( x + 3)( x + 8).

А теперь взгляните на x ² + 9 x = –13. Найти множители для x ² + 9 x + 13 не так-то и просто. Но не отчаивайтесь. В таких случаях на помощь нам придет формула корней квадратного уравнения. Пользу ее переоценить невозможно – вот, смотрите сами:

имеет решение

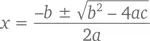
Символ ± означает «плюс» или «минус». Для примера: в уравнении

a = 1, b = 4, c = –12.

Значит, наша формула утверждает, что

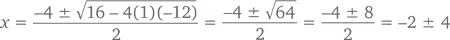
Поэтому x = –2 + 4 = 2 или x = –2 – 4 = –6, что и требовалось доказать. Думаю, вы не станете спорить, что для решения этого примера более уместен был бы метод разложения на множители.

Еще одним забавным способом решения квадратных уравнений является метод дополнения до полного квадрата . Например, чтобы решить уравнение x ² + 4 x = 12, добавим 4 в обе его части, чтобы получить

Сделать это нужно для того, чтобы преобразовать левую часть в ( x + 2)( x + 2). Так наша задачка превращается в

Другими словами, ( x + 2)² = 42. Значит,

что дает нам x = 2 или x = –6, как мы уже выяснили чуть выше.

Но для уравнения

наш выбор очевиден – и это формула корней. У нас получается, что a = 1, b = 9, а c = 13. То есть

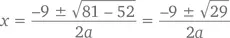
Согласитесь – в общем-то, не самый очевидный случай. По большому счету, в математике очень немного формул, которые действительно надо помнить, но формула корней квадратного уравнения – одна из них. Достаточно немного попрактиковаться, и вы легко обнаружите, что использовать эту формулу просто, как… дважды два.

Почему работает формула корней квадратного уравнения? Давайте запишем уравнение ax ² + bx + c = 0 как

а потом разделим обе части на a (которое не равно 0), чтобы получить

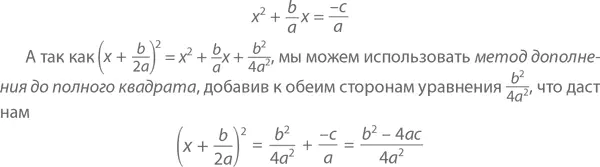
Извлечем квадратный корень из левой и правой частей уравнения:

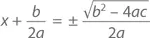
и в результате получим

Что и требовалось доказать.

В XVII веке в математике произошел настоящий прорыв: французы Пьер де Ферма и Рене Декарт независимо друг от друга придумали отличный способ визуализации алгебраических уравнений (равно как и алгебраическую запись геометрических объектов).

Начнем, пожалуй, с графика простого уравнения

Оно означает, что любое значение переменной х мы должны удвоить, а потом прибавить к нему 3 – так у нас и получается y . В таблице ниже приведены несколько возможных пар значений для x и y . Рядом с таблицей – график, на котором все эти значения отмечены точками, и можно легко видеть, что все они определенным образом упорядочены . Посмотрите на координаты: (–3, 3), (–2, –1), (–1, 1) и так далее. Соединив эти точки одной линией и уведя ее в бесконечность, мы получим то, что называется графиком . График рядом с таблицей есть отображение уравнения y = 2 x + 3.

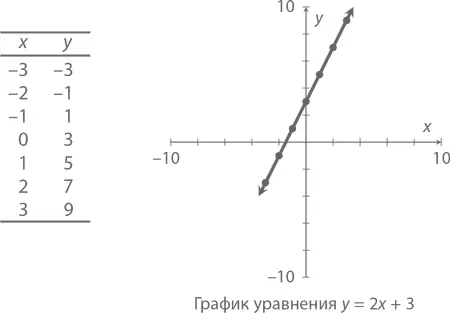
Добавим немного необходимой терминологии. Горизонтальная линия на нашей картинке называется осью X , вертикальная – осью Y . Сам график составляет линия с наклоном 2, которая пересекает ось Y в точке 3. Наклон – это степень «крутизны» линии. Наклон, равный 2, обозначает, что каждый раз, когда x увеличивается на одну единицу, y всегда будет увеличиваться на две (что очень хорошо видно из таблицы). Алгебраически точка пересечения с осью Y – значение y при x = 0. Геометрически же все очевидно: это точка пересечения графика с вертикальной линией. То есть график уравнения

представляет собой линию с наклоном m , которая пересекается с осью Y в точке b (и наоборот). Линия обычно ассоциируется с ее уравнением, Поэтому мы можем просто сказать, что график на предыдущем рисунке – это линия y = 2 x + 3.

А вот график линий y = 2 x – 2 и y = – x + 7:

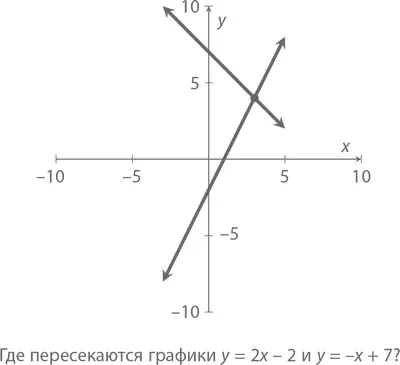
Первая линия y = 2 x – 2 имеет наклон 2 и пересекается с осью Y в точке –2 (график получается параллельным линии y = 2 x + 3 с полным сдвигом вниз по вертикали на 5). Наклон второй линии y = – x + 7 равен –1, поэтому при увеличении x на единицу на ту же единицу уменьшается и y . Призовем на помощь алгебру, чтобы найти точку ( x, y ) пересечения этих двух линий – именно в ней значения наших двух переменных совпадут, и x мы будем искать исходя из того, что он здесь равен y . Иными словами, нам надо решить

Добавим к обеим частям сначала x , потом 2 и получим

то есть x = 3. А зная x , мы можем использовать другое уравнение, чтобы найти y . Если y = 2 x – 2, значит, y = 2(3) – 2 = 4 (а y = – x + 7 дает нам y = –3 + 7 = 4). Значит, графики пересекаются в точке (3, 4).