Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

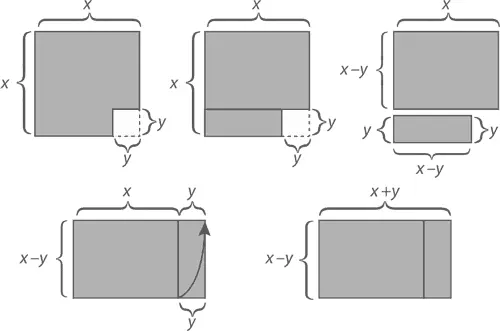
В главе 1 мы научились перемножать между собой близкие по значению числа. Но если там мы оперировали числами, близкими к сотне и начинающимися с одной и той же цифры, то здесь, используя элементы алгебры, мы можем поговорить и о более интересных примерах. Скажем, вот алгебраическая интерпретация метода сближения:

Это становится возможным, потому что ( z + a )( z + b ) = z ² + zb + za + ab , а значит, мы можем вынести за скобки из первых трех элементов сомножитель z . Формула эта работает для любых значений, хотя обычно под z мы понимаем число, заканчивающееся на ноль. Чтобы перемножить, например, 43 × 48, мы берем за z число 40, соответственно, a = 3, b = 8. И тогда наша формула говорит нам, что

Обратите внимание, что при сложении наши множители дают 43 + 48 = 91 – тот же результат, что и менее сложные для подсчетов 40 + 51 = 91. Это совсем не случайно, ведь алгебра говорит нам, что сумма изначальных множителей представляет собой ( z + a ) + ( z + b ) = 2 z + a + b , что является в то же время суммой более простых чисел z и z + a + b . А значит, мы можем легко округлять изначальные числа до удобных нам при подсчетах. Последнее вычисление, например, может быть сведено к z = 50, a = –7 и b = –2, и умножать мы будем 50 на 41. (Легко понять, откуда взялось 41: 43 + 48 = 91 = 50 + 41.) Следовательно,

В главе 1 мы использовали этот метод для чисел больше 100. Но он отлично работает и с меньшими величинами, например,

Обратите внимание, что 96 + 97 = 193 = 100 + 93 (на деле я всего лишь сложил две последние цифры, 6 и 7, чтобы узнать, что сотню нужно умножать на число, заканчивающееся на 3 и, скорее всего, равное 93). Со временем, получив опыт, вы научитесь не обращать внимания на минусы и умножать не отрицательные числа, а их положительные «отражения». То есть

Этот же метод можно применить к парам чисел, одно из которых чуть меньше, а другое – чуть больше 100, только в конце вместо сложения вам нужно произвести вычитание. Например,

И опять же, число 102 можно получить двумя способами: либо из 109 – 7, либо из 93 + 9, либо из 109 + 93 – 100 (ну и четвертый вариант – сложить последние цифры начальных чисел: 9 + 3 скажут нам, что число будет заканчиваться на 2, и этой информации может быть вполне достаточно). Практикуясь, вы научитесь легко перемножать близкие друг к другу числа. Посмотрите на несколько несложных примеров с трехзначными числами. Имейте в виду, что a и b здесь числа, в которых больше одного знака.

Чуть выше мы видели несколько примеров решения уравнений с помощью золотого правила алгебры. Если уравнение содержит только одно неизвестное (скажем, x ) и обе его части – линейные (что значит, что в них есть х или кратные ему величины, но при этом это единственная их сложность – никаких x ²), найти x несложно. Например, чтобы решить уравнение

мы можем к его левой и правой части сначала добавить 7 и получить 9 x = 54, а потом разделить обе части на 9 и получить искомое: x = 6.

Или вот другой пример, чуточку сложнее:

Сначала мы упростим его, убрав из обеих частей 2 x , а потом (ну или вместе с первым шагом, если хотите) 11, что приводит нас к

решением же будет x = 7/3. В конечном итоге любое уравнение можно свести к ax = b (или ax – b = 0) и его решению x = b / a (исходя из того, что a ≠ 0).

Ситуация немного запутывается, если мы имеем дело с квадратным уравнением (в котором на авансцене появляется x ²). Самый простой вариант квадратного уравнения:

которое имеет два решения: x = 3 и x = –3. И даже когда правая сторона уравнения не является квадратом простого числа, вроде

у нас все еще есть два решения: x = √10 = 3,16… и x = – √10 = –3,16… В принципе, если n > 0, число √n – квадратный корень из n – обозначает положительное число с квадратом n . Если n не является квадратом целого числа, √n легче всего посчитать на калькуляторе.

А как насчет уравнения x ² = –9? Пока мы вынуждены сказать, что оно не имеет решения: ведь не существует действительного числа , которое при возведении в квадрат давало бы –9. Но в главе 10 мы увидим, что на самом деле существуют целых два ответа: x = 3 i и x = –3 i , где i – это так называемое мнимое число с квадратом, равным –1. Пусть пока это кажется вам странным и нелепым. Когда-то нам отрицательные числа казались невозможными. (Что это за количество такое – меньше ноля?) А ведь достаточно просто посмотреть на них под правильным углом, чтобы ухватить суть.

Уравнение вроде

выглядит немного сложнее из-за этого 4 x , зато у нас есть несколько способов его решить – ну, к этому мы привыкли, когда считали в уме.

Первый метод, который я обычно применяю в таких случаях, – метод разложения на множители . Сначала перенесем все в левую часть уравнения, чтобы справа остался только 0. Соответственно, наше уравнение превращается в

И что теперь? А теперь вспоминаем последний раздел, где мы говорили о FOIL и где мы уже видели, что x ² + 4 x – 12 = ( x + 6)( x – 2). А это значит, что наше уравнение преобразуется в

Единственная возможная ситуация, в которой произведение двух сложных множителей равно 0, – это когда один из них равен 0. Следовательно, у нас либо x + 6 = 0, либо x – 2 = 0, то есть