Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Зная две точки, лежащие на одной прямой, нарисовать график в виде целой линии становится делом техники. Немного сложнее иметь дело с квадратичной функцией (и фигурирующим в ней x ²). Самое простое для отображения в виде графика – уравнение y = x ² (изображен ниже). Подобные графики называются параболами .

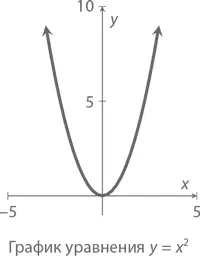
А вот график уравнения y = x ² + 4 x – 12 = ( x + 6)( x – 2).

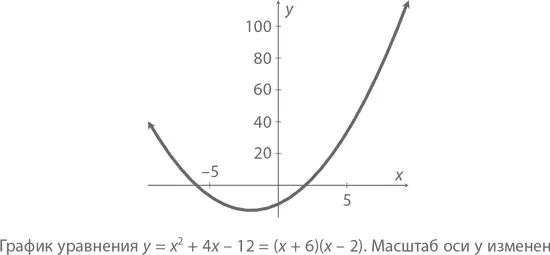
Обратите внимание, что, когда x = –6 или x = 2, y = 0. Это легко заметить на графике – в тех двух его местах, где парабола пересекает ось x . И совсем не случайно, что самая нижняя ее точка располагается точно в центре между ними – при x = –2 и y = –16. Это вершина .

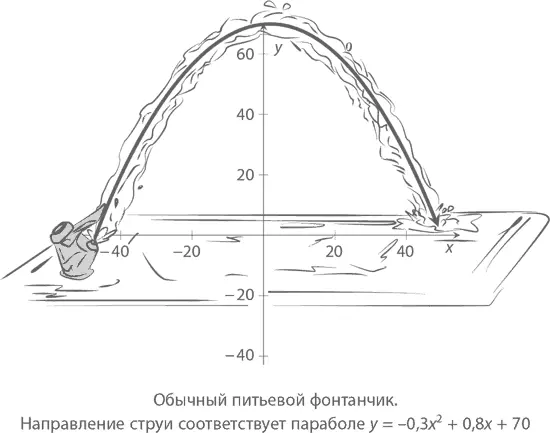
С параболами мы сталкиваемся каждый день. Каждый раз, когда вы видите движущийся по кривой предмет, будь то летящий мяч или струя воды в фонтанчике, вы, в сущности, видите параболу (просто взгляните на картинку чуть ниже). Свойства параболы активно используются в устройстве фар, телескопов, спутниковых тарелок и многих других приборов.

Еще немного терминологии. До этого все наши примеры содержали в себе многочлены – комбинации чисел и одной переменной (скажем, x ), которая может быть возведена в положительную целую степень. Наибольшую из степеней входящего в многочлен одночлена называют степенью многочлена . Например, 3 x + 7 – это (линейный) многочлен первой степени. Многочлен второй степени, вроде x ² + 4 x – 12, называется квадратным , многочлен третьей степени (5 x ³ – 4 x ³ – √2) – кубическим . Бывают многочлены и других, бóльших, степеней (я, правда, никогда не слышал их специальных названий – главным образом, думаю, потому, что не так уж и часто они встречаются. Интересно, насколько часто используются в профессиональной литературе термины «квартический», «квинтический» и т. п. многочлены? Встречаются, наверное, но я, честно говоря, по этому поводу настроен немного скептически). А еще бывают многочлены, в которых нет переменных (например, 17) – о таких говорят, что они стоят в нулевой степени . Ну и последнее, что вам нужно знать о многочленах – это то, что многочленом не может быть сочетание с бесконечным количеством чисел. Например, 1 + x + x ² + x ³ +… – не многочлен, а так называемый бесконечный ряд , о которых мы поговорим подробнее в главе 12.

Обратите внимание, что в случае с многочленами степень, в которую возводятся переменные, может быть выражена только положительным целым числом – ни в коем случае не отрицательным и не дробным. То есть если вам попадается уравнение с чем-нибудь вроде y = 1/ x или y = √ х , это не многочлен, потому что 1/ x = x –1, а √ х = x ½.

Корнями многочлена мы считаем такие значения х , при которых многочлен равняется 0. Например, 3 x + 7 имеет один корень, а именно x = –7/3. А вот у x ² + 4 x – 12 два корня: x = 2 и x = –6. А x ² + 9 корня (в смысле, действительного корня) не имеет вообще. Обратите внимание, что каждый многочлен степени 1 ( линейный ) имеет один корень в силу того, что он пересекает ось X только в одной точке, квадратный – не больше двух. Многочлены x ² + 1, x ² и x ² – 1 имеют соответственно ноль, один и два корня.

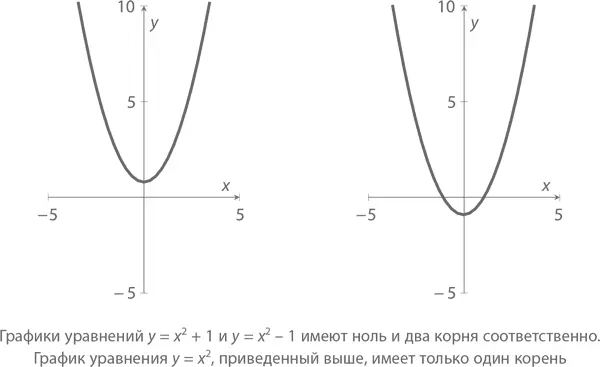
А вот графики двух кубических многочленов, на которых вы легко заметите, что в обоих – максимум три корня.

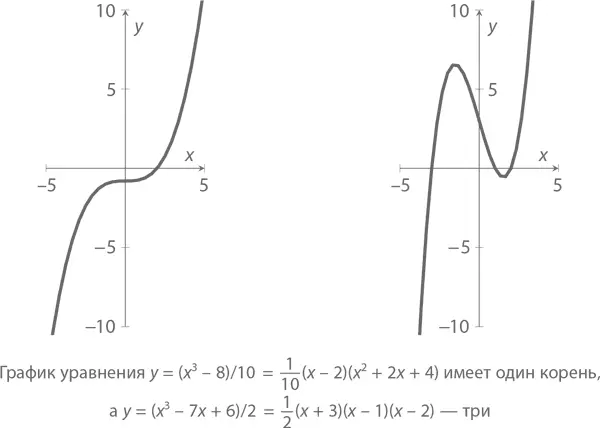
В главе 10 мы рассмотрим основную теорему алгебры , которая гласит, что каждый многочлен, возведенный в степень n , имеет не более n корней. Более того, он может быть разложен на линейную и квадратную части. Например,

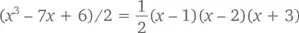
имеет три корня (1, 2 и –3). В свою очередь,

имеет только один действительный корень – при x = 2 (и еще два комплексных , но им придется подождать до главы 10). Сегодня, кстати, очень легко можно найти график практически любой функции, просто набрав нужное вам уравнение в своем любимом поисковике. Просто напечатайте что-нибудь вроде y = (x^3 – 7 x + 6)/2, и получится рисунок наподобие тех, которые представлены в этой книге.

В этой главе мы научились легко находить корни любого линейного или квадратного многочлена. А еще есть формулы для нахождения корней многочленов третьей или четвертой степеней, но они очень-очень сложные. Вывели их еще в XVI веке, а потом еще две сотни лет ведущие математики занимались поиском такого же уравнения для многочлена пятой степени. Лучшие умы бились над этой проблемой и никак не могли найти решения, пока в начале XIX века норвежский математик Нильс Абель не доказал, что создать такую формулу для пятой и более высокой степени просто-напросто невозможно. Это приводит нас к каламбуру, который считают забавным только математики: «Почему Исаак Ньютон не смог доказать теорему невозможности формулы для пятого порядка? – Потому что корни с деревьев не падают!»

Примеры доказательств невозможности чего-либо мы рассмотрим в главе 6.

Почему x –1= 1/ x ? Конкретнее, почему 5 –1= 1/5? Взгляните на такую закономерность:

Обратите внимание, что с каждым уменьшением степени на единицу число делится на 5, что имеет для нас смысл, если над этим задуматься. Ведь тогда 5 0= 1, 5 –1= 1/5, 5 –2= 1/25 и так далее. Настоящая же причина этого – правило действий со степенями, согласно которому x a x b= x a+b. Лучше всего он работает, когда a и b – положительные и целые величины. Так, x ² = x · x , а x ³ = x · x · x . Значит,

Если мы хотим, чтобы правило работало при значении степени, равном 0, необходимо, чтобы

а так как левая часть становится равна x a, этому же значению должна быть равна правая часть, что возможно только при x 0= 1.