Владимир Менделев - Энциклопедия игр

Фигуры, которые можно уложить из прямоугольного танграма (рис. 193), можно увидеть на рис. 195.

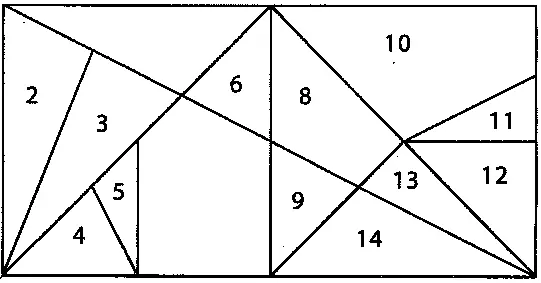
Танграм, изображенный на рис. 194, носит название «яйцо Колумба».

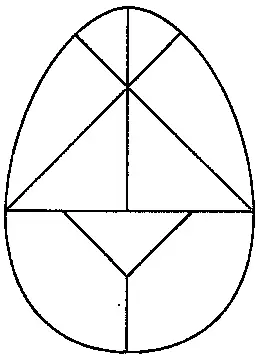
Некоторые фигуры, которые можно выложить из «яйца Колумба», показаны на рис. 196.

На рис. 301–310 приведены решения некоторых задач танграма.

Придумана в 1878 году американским шахматистом и изобретателем Сэмюэлем Ллойдом. Математическую теорию игры разработали в 90-х годах прошлого века математики Джонсон и Стори. Игра сразу приобрела популярность и пользуется ею до сих пор. В США ее называют «boss puzzle» (загадка для боссов), во Франции — «таким» и т. д. Пик ее известности приходится на конец XIX века, когда игре в пятнадцать посвящались даже фельетоны и карикатуры.

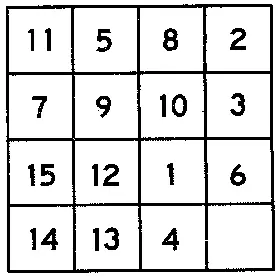
Реквизит.Плоская квадратная коробочка и в ней пятнадцать нумерованных квадратных фишек (от единицы до пятнадцати), размещенных с небольшим зазором — так, чтобы фишки могли перемещаться (рис. 197).

Надо высыпать квадратики из коробочки, перемешать их и вновь разместить там так, как придется. Затем, передвигая квадратики (используя свободное место), надо восстановить правильный порядок чисел или перейти к новому, заданному заранее (например, от расположения, показанного на рис. 198, к исходному).

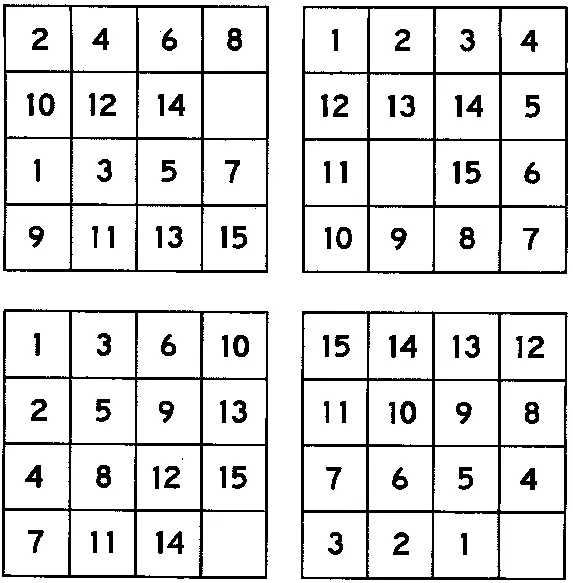
Существует множество вариантов расположения квадратиков, которые нужно получить в результате игры: четные, нечетные, по спирали, по диагонали, в обратном порядке и т. д.

Некоторые из возможных расположений квадратиков показаны на рис. 199.

Обладая двумя или более комплектами для игры, можно играть с партнерами, например, на время.

Среди многих вариантов игры в пятнадцать, появившихся позже и основанных на том же принципе, стоит отметить два.

В коробочке несколько измененной формы располагается девятнадцать квадратиков — шестнадцать нумерованных и три — отмеченных нулем. Одно место свободно (рис. 200).

Все остальные правила игры — без изменений.

Английский вариант

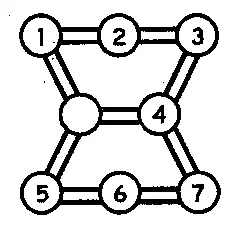
В коробочке специфической формы лежат семь пронумерованных фишек. Одно место свободно. Возможный «маршрут» пешек обозначен двойной линией. Все остальные правила игры те же (рис. 201).

Головоломка с перемещением фигур внутри прямоугольной рамки (4×5), разработанная швейцарцем Вальдемаром Шейером в 1982 году (рис. 202).

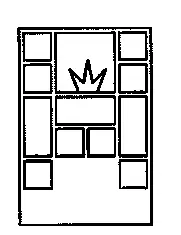
Задача — перевести корону в нижний ряд.

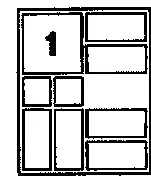
Головоломка подобна предыдущей. Задача — привести фигуру один в правый нижний угол (рис. 203).

Современная игра-головоломка, название которой дал американский математик С. В. Голомб в 1953 году. В Великобритании известна как «maestro puzzle» («загадка мастера»).

Разными аспектами пентамино занимались Р. М. Робинсон, Мартин Гарднер, Д. Клернер и многие другие. В свое время много места отводил ей на своих страницах журнал «Наука и жизнь», печатая не только задачи пентамино и их решения, но и достаточно глубокие исследования на эту тему, а также новые игры, основанные на тех же принципах, но с другим числом фигур (гексамино, декамино и т. д.) или с пространственными фигурами.

Реквизит.12 плоских геометрических фигур (камней) одинаковой площади (составленные из пяти основных квадратиков), но совершенно разной формы.

Камни обычно называют по той латинский букве, которую они напоминают.

Полный комплект камней пентамино показан на рис. 204.

В случае необходимости всегда можно перевернуть любой камень.

Основная задача игры пентамино — построить различные прямоугольники, реже — другие фигуры.

Вот несколько задач. Следует выложить:

прямоугольник размерами 6×10 (малых квадратов). Задача имеет 2339 разных решений;

прямоугольник 4×15 (368 решений); прямоугольник 5×12 (1010 решений); прямоугольник 3×20 (два решения).

Задачи эти можно усложнить, например, так:

построить прямоугольник 6×10 так, чтобы каждый камень касался наружного контура;

сложить такой же прямоугольник так, чтобы определенный камень не касался наружного контура; выложить квадрат 5×5 и прямоугольник 5×7;

образовать два одинаковых прямоугольника 6×5 (два решения);

выложить прямоугольник 6×10, предварительно установив положение одного из камней (рис. 205);

построить квадрат 8×8 с квадратным отверстием 2×2 в центре;

образовать квадрат 8×8 с отверстием 2×2, расположенным в заранее указанном месте большого квадрата (задача всегда имеет решение).

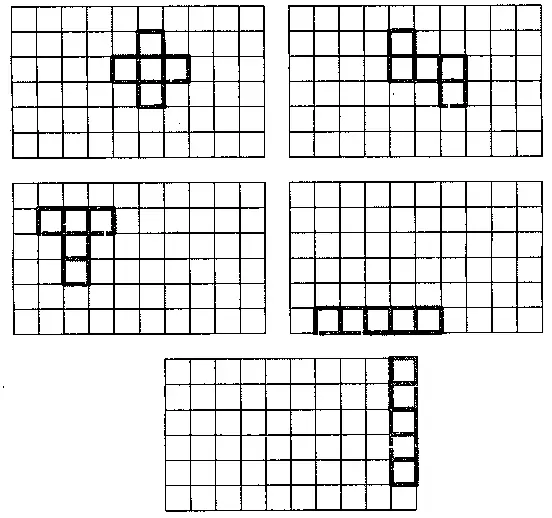
Можно из комплекта камней построить и другие фигуры (рис. 206–208).