Дарья Нестерова - Энциклопедия лучших игр со словами и цифрами

Два города, A и B, находятся на расстоянии 30 км друг от друга. Из этих городов одновременно выходят друг другу навстречу два пешехода и движутся, не останавливаясь, каждый со скоростью 5 км/ч. Но вместе с первым пешеходом из города A вылетает оса, пролетающая в час 10 км.

Она опережает первого пешехода и летит навстречу второму, вышедшему из города B. Встретив его, она сразу поворачивает назад, к пешеходу, движущемуся из города A. Повстречав его, оса снова летит обратно навстречу второму пешеходу. Она продолжала свои полеты вперед и назад до тех пор, пока пешеходы не встретились. Тогда она успокоилась и села на дерево. Сколько километров пролетела оса?

Ответ

Оса, не останавливаясь, летала ровно 3 часа, а значит она пролетела 30 км.

Условие

Сколько детей в многодетной семье, если известно, что у каждого сына сестер столько же, сколько и братьев, а у каждой дочери братьев вдвое больше, чем сестер?

Сколько братьев и сестер в многодетной семье?

Ответ

В многодетной семье 7 детей – 4 сына и 3 дочери.

Условие

Этому парню по имени Иван не позавидуешь. Вот уже много лет подряд его дед Никита мучиет его одним и тем же фокусом. Как только наступает день рождения внука, старый скупердяй предлагает ему следующее: дав Ивану десять долларовых купюр и десять стодолларовых, он просит разложить их в две одинаковые коробочки.

После этого дед завязывает внуку глаза и несколько раз передвигает коробочки по столу так, чтобы Иван не догадался, где какая. Если внук кладет стодолларовые купюры сверху, вредный старик еще и перемешивает их в коробочке. Затем дед позволяет Ивану вытащить единственную купюру, которая чаще всего оказывается долларовой.

Каким образом Иван может увеличить свои шансы на успех и вытащить стодолларовую купюру?

Сгибать, надрывать, сминать и складывать купюры пополам Ивану не разрешается.

Ответ

Ивану следует положить стодолларовую купюру в одну коробочку, а все остальные – в другую, после чего его шансы попасть в коробочку с заветной купюрой оцениваются как 50 на 50.

Но если он запустит руку в коробочку с девятнадцатью купюрами, то его шансы выудить стодолларовую составят 9 из 19. Поэтому в целом вероятность того, что Иван достанет желанную купюру, можно определить так:

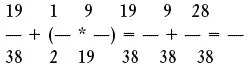
Это означает, что шансы Ивана вытаскивать ежегодно на свой день рождения по стодолларовой купюре равны 0,7368, или примерно 74%.

Условие

Звезды балета, сестры Ирина и Елена, вовсе не собирались открывать поклонникам свой возраст.

Их пресс-секретарь на вопрос репортеров о возрасте сестер сказал следующее: «Если сложить возраст обеих сестер, в сумме получится 44.

Сейчас Ирине вдвое больше, чем было Елене, когда Ирине было наполовину столько же, сколько будет Елене, когда она станет вдвое старше, чем была Ирина тогда, когда ей было в три раза больше, чем тогда Елене».

Сколько лет сестрам?

Ответ

Чтобы ответить на этот вопрос, следует начать решение задачи с конца. Когда Елене было 5,5 лет, Ирине было 16,5 лет, когда Елене будет в три раза столько же, то есть 49,5 лет, то, разделив это число пополам, получим 24 и 3/4. Когда Ирине было столько лет, Елене было 13 и 3/4 лет. Следовательно, возраст Ирины в два раза больше, то есть 27,5 лет. Теперь нетрудно узнать возраст другой сестры: 44 – 27,5 = 16,5.

Условие

На рисунке 44 числа 1, 18, 17 и 14 стоят в углах воображаемого квадрата и дают в сумме 50. Найдите квадрат (любого размера) с числами, стоящими в его углах, которые давали бы максимальную сумму.

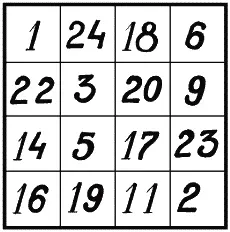
Рис. 44. Числа в углах квадрата, дающие в сумме 50

Ответ

Максимальная сумма чисел, находящихся в углах квадрата, равна 82 (рис. 45).

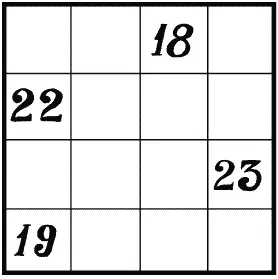
Рис. 45. Квадрат с числами в углах, сумма которых равняется 82

Условие

Попрыгунья – стрекоза 1/2 каждых суток лета спала, 1/3 каждых суток танцевала, 1/6 часть – пела. Остальное время она решила посвятить подготовке к зиме.

Сколько часов в сутки стрекоза готовилась к зиме?

Ответ

На подготовку к зиме у стрекозы не оставалось времени.

Условие

Циферблат часов (рис. 46) разбился на четыре части так, что сумма римских чисел на каждом куске стала равняться двадцати.

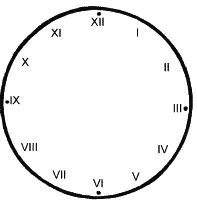
Рис. 46. Циферблат

Определите, как треснул циферблат.

Ответ

Ответ показан на рисунке 47.

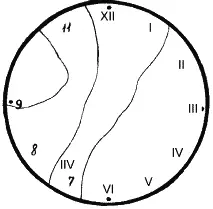
Рис. 47. Разбитый циферблат

Условие

Назовите состоящие из одинаковых цифр числа, сумма которых равна их произведению. При этом числа должны состоять не менее, чем из двух цифр.

Ответ

Это числа 11 и 1,1. При сложении и перемножении результат равен 12,1.

Условие

В углах квадрата со стороной 10 см находится по таракану.

Если все четыре насекомых начнут двигаться одновременно и с постоянной скоростью, каждый – по одной из сторон квадрата по направлению к другому таракану (по часовой стрелке), то какое расстояние преодолеет каждый из них до того момента, когда тараканы встретятся?

При этом следует помнить, что тараканы всегда ползут по кратчайшему пути к своей цели. Для точности следует принять тараканов за безразмерную точку.

Ответ

В любой момент времени таракан-преследователь ползет по направлению, перпендикулярному пути преследуемого насекомого. По этой причине последнее никак не может оторваться от преследователя или приблизиться к нему. А таракану-преследователю нужно преодолеть лишь те самые 10 см, которые разделяли их в самом начале.

Условие

На столе лежит колода карт, все карты на месте. Игроки по очереди берут из колоды произвольное количество карт, но не более трех. Выигрывает тот, кто забрал из колоды последние карты (или карту).

В одном из розыгрышей победил участник, который ходил первым, причем он был уверен в выигрыше с самого начала.