Александр Ромашов - Стратегии развития научно-производственных предприятий аэрокосмического комплекса. Инновационный путь

Допустим, что ориентировочно известны интервал объема выпуска продукции по каждой позиции номенклатуры и соответствующая цена. Обозначим нижнюю границу интервала значений объема выпуска i -го изделия символом n i , а верхнюю – N i . Тогда ограничение 1 в модели будет иметь следующий вид: x i ≥ n i,, x i < N i, i = 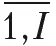. Такое преобразование переводит ограничение 1 в линейную область.

Аналогично преобразуется к линейному виду ограничение 2. Зафиксируем технологический процесс обработки деталей g -й группы. Тогда автоматически фиксируется и уровень автоматизации r используемого в этом технологическом процессе оборудования. Такая фиксация не означает, что все технологическое оборудование j -й группы будет иметь один и тот же уровень автоматизации. Напротив, разбиение технологического оборудования на группы станет более мелким, а понятие группы оборудования приобретет большую детализацию. Это означает, что элементы j -й группы технологического оборудования с разным уровнем автоматизации будут теперь относиться к разным группам оборудования. Таким образом, индексы k и r в модели из рассмотрения исключаются, а ограничение 2 примет следующий вид:

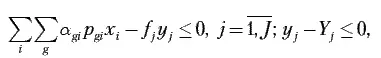
где α gj – трудоемкость обработки деталей – представителей g -й группы на j -й группе технологического оборудования в новой трактовке этой группы.

Переменная y j во вновь сформулированном ограничении приобретает новый смысл. Она будет означать не искомое количество технологического оборудования j -й группы для выполнения программы производства, а используемое количество оборудования этой группы. При этом величина y j заранее ограничивается наличным или допустимым к использованию количеством оборудования в данной группе Y j .

Ограничение 3 по производственной площади приобретет смысл определения потребности предприятия в производственной площади, необходимой для размещения используемого технологического оборудования, и будет иметь следующий вид:

∑ js jy j– S = 0.

Привести ограничение 4 к линейному виду невозможно. Если исключить булеву переменную δ jr под знаком ∑, то это приведет к неоправданному сложению затрат на расширение j -й группы технологического оборудования и «экономии» на уменьшении ее состава. Причем обе эти величины будут рассчитаны по цене покупки. Аналогично второй элемент суммы будет учитывать те же затраты, только с обратным знаком по цене реализации излишков оборудования предприятия. Такой подход искажает реальную ситуацию. Исключение ограничения 4 из модели означает, что активная часть производственных фондов не преобразуется в процессе обновления производства.

Допустив, что активная часть производственных фондов предприятия не изменяется, мы расширили номенклатуру производимой продукции. В этом случае вопрос о дополнительных капитальных вложениях из рассмотрения также исключается. При этом проблемы о возможном расширении производственных площадей и о дополнительных капитальных вложениях решаются административными методами. Соответственно, в модели критерий оптимальности приобретет следующий вид:

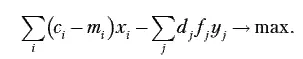
где d j – затраты в расчете на один машино-час содержания и эксплуатации оборудования j -й группы;

f j – годовой фонд времени работы единицы оборудования j -й группы.

Анализируя полученный критерий оптимальности, можно заметить, что по отношению к первоначальному виду он изменился не только по форме, но и по содержанию. Теперь вместо максимума чистого дисконтированного дохода требуется обеспечить максимум прибыли предприятия. Такая трансформация критерия оптимальности естественна, если учесть, что объем капитальных вложений был зафиксирован путем исключения из рассмотрения ограничения 4 по объему дополнительных капитальных вложений. Тогда окончательно упрощенная экономико-математическая модель будет иметь следующий вид.

Ограничениями экономико-математической модели являются:

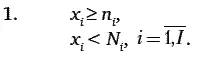
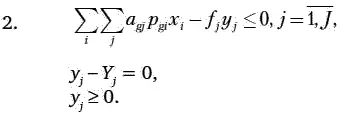
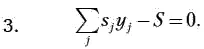
Критерий оптимальности экономико-математической модели:

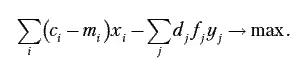
В такой записи экономико-математическая модель обновления производства становится линейной. Добавив к этой модели требование xi, yj – целые, для решения можно использовать существующие алгоритмы целочисленного программирования.

При приведении модели обновления производства к реализуемому виду из нее были исключены факторы, ограничивающие дополнительные капитальные вложения, а также затраты на использование привлеченного со стороны капитала и его возмещение. В окончательном виде экономико-математическая модель представляет собой модель баланса производственных ресурсов предприятия. С использованием методов планирования эксперимента эта модель может быть применена на практике для решения конкретных задач формирования конкурентной стратегии предприятия.

В результате инновационной деятельности НПП научные знания преобразуются в инновацию, являющуюся объектом интеллектуальной собственности. Этот процесс можно представить в виде последовательности событий, в результате свершения которых инновация из идеи превращается в конкретный продукт (продуктовую инновацию) и технологию его изготовления (процессную инновацию), а затем переходит в сферу практического использования. Инновационный процесс не прекращается и после промышленного освоения инновации, поскольку по мере распространения технологическая инновация совершенствуется, становится более эффективной. В настоящее время в промышленно развитых странах на долю новых знаний, воплощенных в технологиях, оборудовании и продукции, приходится до 85 % прироста ВВП. Ведущее положение в мире по этому показателю занимают США. Так, в 2000 г. совокупные затраты на НИОКР в США составили $250 млрд, превысив расходы на эти цели Японии, Южной Кореи, Великобритании, Франции, ФРГ, Италии и Канады, вместе взятых.