Александр Ромашов - Стратегии развития научно-производственных предприятий аэрокосмического комплекса. Инновационный путь

d ≥ T з.

Теперь допустим, что станки комплекта обслуживаются в порядке присвоенных им номеров. В случае одновременного окончания автоматической работы нескольких станков они будут обслуживаться в том же порядке, т. е. предпочтение будет отдано станку с меньшим номером. Построим доказательство от противного.

Допустим, что пропорциональность операций не гарантирует бесперебойной работы комплекта, т. е. через некоторое время T от момента t =0 начала работы комплекта возникает простой одного из станков по причине, что в этот момент рабочий занят обслуживанием другого станка. Эта ситуация включает и вариант одновременной остановки станков. Обозначим номера рассматриваемых станков соответственно k и q и предположим, что k < q . Пусть к моменту времени T операция k выполнялась N k раз. Тогда из пропорциональности операций следует, что операция q выполнялась

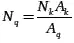
раз.

Следовательно, простой станка q может возникнуть при условиях, описываемых системой неравенств следующего вида:

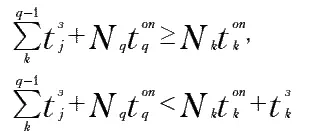
а простой станка k – при условиях, описываемых системой аналогичных неравенств следующего вида:

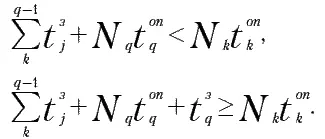
Учитывая, что

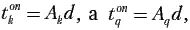
из первой системы неравенств имеем:

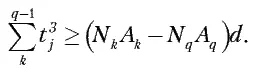
Используя выражение для N q , получаем, что

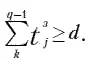
Тогда тем более T з > d . Это противоречит основному условию МСО, хотя ранее мы приняли, что оно должно выполняться.

Аналогичный результат можно получить, используя условия второй системы неравенств. Значит, предположение о возможности простоев станков в комплекте, выполняющем пропорциональные операции, при соблюдении основного условия МСО неверно. Таким образом, доказана достаточность требования пропорциональности операций для бесперебойной работы комплекта. Заметим, что величина

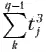
представляет собой сдвиг по времени момента начала первого обслуживания станка q по отношению к началу первого обслуживания станка k . Поскольку номера k и q выбраны произвольно, то принятое при доказательстве упорядочение станков не влияет на его общность.

Случай пропорциональных операций имеет большую общность по сравнению со случаем кратных операций. Случай кратных операций получается из случая пропорциональных операций при условии, что любое A j+1 = A jb j+1 , где b j+1 – натуральное число.

Это является существенным ограничением на организацию МСО. Требование пропорциональности операций можно сформулировать в виде делимости всех оперативных времен выполняемых в комплекте МСО операций на минимальное значение оперативного времени.

Удобство пропорциональных операций состоит в том, что для них можно аналитически рассчитать характеристики комплекта МСО, которые обычно определяются с помощью циклограммы. К таким характеристикам прежде всего относится величина цикла МСО. Под циклом МСО понимается минимальный интервал времени, в течение которого обслуживание всех станков комплекта повторяется в одинаковом порядке.

При пропорциональных операциях величина цикла МСО составит

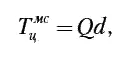
где Q – наименьшее общее кратное коэффициентов Aj .

Из данного соотношения можно вычислить коэффициент загрузки рабочего. За время цикла МСО j -я операция выполняется Q / A j раз. При каждом ее выполнении рабочий затрачивает время t з j . Следовательно, общая загрузка рабочего в цикле МСО будет равна

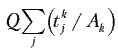
а коэффициент загрузки рабочего составит

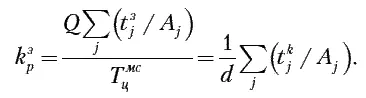
На базе случая пропорциональных операций удобно построить некоторые приближенные алгоритмы создания комплектов для МСО при роботизированном обслуживании станков.

Задача организации МСО в роботизированном производстве при проектировании роботизированных организационно-производственных структур и в процессе их эксплуатации формулируется по-разному. На этапе проектирования требуется найти оптимальное разбиение всего множества станков организационно-производственной структуры на комплекты для МСО, каждый из которых обслуживается одним роботом.

В процессе эксплуатации организационно-производственных структур задача организации МСО наиболее актуальна для диверсифицированного производства. Решить ее можно, оптимально закрепив операции за существующими роботизированными организационно-производственными структурами на очередной плановый период. Это может быть смена, сутки или какой-либо другой календарный отрезок времени. В любом случае речь идет о взаимозаменяемых станках по отношению к номенклатуре выполняемых операций. Если это условие выполняется не для всех станков организационно-производственной структуры, задачу следует решать по отношению к каждой группе взаимозаменяемого оборудования.

При постановке задачи организации МСО следует также учитывать, что некоторые типы промышленных роботов не обладают свободой перемещения. Поэтому для стационарных роботов существует ограничение на количество станков рассматриваемого типа в зоне обслуживания каждого робота. Задача организации МСО в диверсифицированном производстве усложняется. Это связано с тем обстоятельством, что плановый объем работ по некоторым операциям может не обеспечивать полной загрузки станков. Поэтому каждая из заданных к выполнению операций в оперативном времени работы станка кроме величин t on j и t з j должна характеризоваться плановым коэффициентом загрузки станка K з j .