Александр Ромашов - Стратегии развития научно-производственных предприятий аэрокосмического комплекса. Инновационный путь

Задача разбиения группы взаимозаменяемых станков организационно-производственной структуры на комплекты для роботизированного варианта МСО на этапе проектирования может быть сформулирована следующим образом:

● даны М станков, за каждым из которых закреплено выполнение операции с известными значениями величин t on j, t з j и K з j ;

● известно максимально допустимое количество станков r в зоне обслуживания каждого промышленного робота (для робота с неограниченной зоной обслуживания можно предположить, что r = M ).

В результате решения задачи требуется найти такое разбиение заданного множества станков на комплекты для МСО, чтобы достигался оптимум выбранной целевой функции при условии, что фактический коэффициент загрузки любого из станков k з j при работе в комплекте для МСО удовлетворяет условию

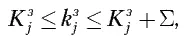
где Σ – заданная величина.

В качестве целевой функции эффективности организации МСО могут выступать различные функциональные зависимости, характеризующие процесс формирования экономических и финансовых показателей. Например, на практике таким показателем часто служит минимум затрат на приобретение и использование робототехники и технологического оборудования.

В процессе эксплуатации роботизированного производства формулировка задачи организации МСО приобретает другой вид:

● даны N комплектов станков для МСО и M операций, подлежащих выполнению в плановом периоде, которые характеризуются теми же параметрами, что и в предыдущем случае. Причем величина М не должна превышать значение суммарного числа станков во всех комплектах.

В результате решения данной задачи требуется закрепить операции за комплектами таким образом, чтобы минимизировать текущие затраты на содержание и эксплуатацию роботизированной организационно-производственной структуры при тех же, что и в предыдущем случае, требованиях к величине k з j . Эти требования формализуют условия обязательного выполнения планируемой производственной программы организационно-производственной структуры.

Сформулированные задачи организации МСО являются комбинаторными. Точное решение таких задач можно получить только путем полного перебора всех возможных вариантов группировки станков в комплекты или путем проектирования всех возможных вариантов закрепления операций за станками. При достаточно большом количестве станков такие задачи относятся к классу труднорешаемых, т. е. их решение нельзя получить за приемлемое время даже с помощью компьютерных программ.

Разработка приближенных методов решения комбинаторных труднорешаемых задач представляет практический интерес. Мы разработали один из таких методов и довели его до практической реализации.

Идея предлагаемого метода решения основана на аналогии со случаем пропорциональных операций. Пусть даны М операций, характеризующихся величинами t j on, t j з и K j з . Допустимое превышение загрузки станков по отношению к плановой величине составляет Σ. Требуется закрепить заданное количество технологических операций за комплектами для МСО таким образом, чтобы фактически коэффициенты загрузки станков были не меньше планируемых и отличались от них не больше чем на величину Σ.

Для всех заданных операций рассчитываются величины τ j = [ t j on ], где символ [ ] означает целую часть числа. По смыслу τ j представляет собой период повторяемости j операции, при котором коэффициент загрузки выполняющего эту операцию станка с точностью до округления результата деления равен K j з .

Примем d = min τ j

Рассчитанные периоды повторяемости проверяются на пропорциональность. Для этого по каждой операции определяется, во-первых, величина

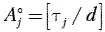
а во-вторых, фактический коэффициент загрузки k з j при выполнении данной операции в комплекте для МСО с коэффициентом пропорциональности d . Очевидно, что в этом случае

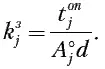
Технологическая операция может быть выполнена в выбранном комплекте для МСО при условии, что k з j находится в пределах допустимого отклонения Σ от K j з . Окончательная проверка допустимости выбора комплекта станков для организации МСО заключается в контроле основного условия МСО: T з = d .

В том случае, если T з > d , то количество станков в комплекте необходимо уменьшить. Аналогично количество станков в комплекте МСО не может превышать допустимое количество станков в зоне обслуживания выбранного промышленного робота.

Для реализации метода аналогии с пропорциональными операциями можно построить соответствующий алгоритм вычислений. При создании такого алгоритма задача разбиения заданного множества станков на комплекты для МСО заменяется задачей последовательного выделения таких комплектов. В этом случае для всех заданных к выполнению операций вначале рассчитывается период повторения τ j . После этого операции упорядочиваются в соответствии с возрастанием τ j , а затем осуществляется пошаговый процесс выделения комплектов. На каждом шаге за величину d следует принимать значение τ j з для первой в последовательности операции. Далее к выбранной операции следует подбирать другие операции, исходя из их пропорциональности, допустимости величины k j з и ограничений по основному условию МСО и количеству станков в зоне обслуживания робота.

Очевидно, что величина параметра Σ влияет на подбор технологических операций, включаемых в комплекты МСО. Путем вариации данного параметра в некоторых, допустимых с точки зрения заданных условий проектирования роботизированного производства, пределах можно получить различные варианты организации МСО. Каждому из таких вариантов будет соответствовать определенное значение выбранной при постановке задачи целевой функции эффективности. Выбор варианта, обеспечивающего оптимум целевой функции, позволяет говорить о квазиоптимальном характере приближенного метода.

Предложенный метод может быть использован при постановке и решении задачи о выборе модели промышленного робота для обслуживания данной группы взаимозаменяемого оборудования. Действительно, если с технической и технологической точки зрения допустимо обслуживание оборудования различными промышленными роботами, то, решая задачу организации МСО и выбирая квазиоптимум для каждой модели робота, можно затем сравнить их между собой на основании квазиоптимумов целевой функции. В результате сравнения выбирается та модель робота, которая обеспечивает оптимизацию характеристик проектируемой системы.