Леонид Букин - Статистика: учебное пособие

Согласно теории типологических группировок, решающее значение в оценке однородности совокупности принадлежит не форме распределения, а размеру вариации и условиям ее формирования. Для качественно однородной совокупности характерна вариация в определенных пределах, после чего начинается новое качество. Вместе с тем к этим границам для оценки качественной однородности совокупности надо подходить с точки зрения существа дела, а не формально, так как одно и то же количество в разных условиях выражает новое качество. Например, при одной и той же численности рабочих предприятия одних отраслей промышленности являются крупными, а других – мелкими.

Для всестороннего и углубленного изучения явлений, для объективной характеристики типов явлений, их взаимоотношений и процессов, обусловленных развитием системы как целого, необходимо сочетать групповые средние с общими средними. Сочетание таких средних и является одним из основных элементов анализа сложных систем. Это сочетание связывает в одно целое два органически дополняющих друг друга статистических метода: метод средних величин и метод группировки. При расчете средней индивидуальные варьирующие по группе значения заменяются одним средним значением. При этом случайные отклонения значения признака по отдельным единицам в сторону увеличения или уменьшения взаимно уравновешиваются и погашают друг друга, а в величине средней проявляется типичный размер признака, свойственный данной группе. Средняя величина служит характеристикой совокупности и в то же время относится к отдельному ее элементу – носителю качественных особенностей явления. Значение средней вполне конкретно, но одновременно и абстрактно; оно получено путем абстрагирования от случайного индивидуального по каждой единице с целью выявления того общего, типичного, что свойственно всем единицам и что формирует данную совокупность. При расчете средней величины численность единиц совокупности должна быть достаточно большой. Величина средней определяется как отношение общего объема явлений к числу единиц совокупности в группе. Для несгруппированных данных это будет средняя арифметическая простая:

а для сгруппированных данных, где каждое значение признака имеет свою частоту, – средняя арифметическая взвешенная:

где X i – значение признака; f i – частота этих значений признака.

Поскольку средняя арифметическая рассчитывается как отношение суммы значений признака к общей численности, она никогда не выходит за пределы этих значений. Средняя арифметическая обладает рядом свойств, которые широко используются в целях упорядочения расчетов.

1. Сумма отклонений индивидуальных значений признака от средней величины всегда равна нулю:

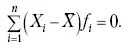
Доказательство. n

Разделив левую и правую часть на

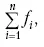
получим:

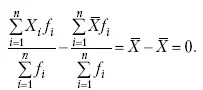
2. Если значения признака (X i) изменить в k раз, то средняя арифметическая также изменится в x раз.

Доказательство.

Среднюю арифметическую из новых значений признака обозначим X, тогда:

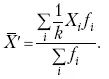
Постоянную величину 1/ k можно вынести за знак суммы, и тогда получим:

3. Если из всех значений признака X i вычесть или прибавить одно и то же постоянное число, то средняя арифметическая уменьшится или увеличится на эту величину.

Доказательство.

Средняя из отклонений значений признака от постоянного числа будет равна:

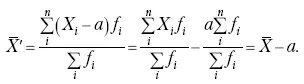
Точно так же доказывается это и в случае прибавления постоянного числа.

4. Если частоты всех значений признака уменьшить или увеличить в n раз, то средняя не изменится:

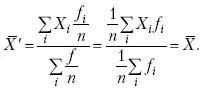
При наличии данных об общем объеме и известных значениях признака, но неизвестных частотах для определения среднего показателя используют формулу среднеарифметической взвешенной.

Например, имеются данные о ценах реализации капусты и общей выручке за различные сроки реализации (табл. 1).

Таблица 1.

Цена реализации капусты и общая выручка за различные сроки реализации

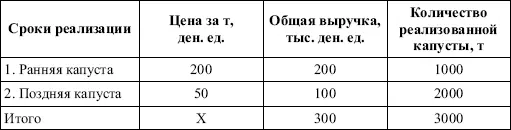
Так как средняя цена представляет отношение общей выручки к общему объему реализованной капусты, то вначале следует определить количество реализованной капусты по разным срокам реализации как отношение выручки к цене, а затем уже определить среднюю цену реализованной капусты.

В нашем примере средняя цена будет:

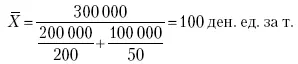
Если рассчитать в данном случае среднюю цену реализации по средней арифметической простой, то получим иной результат, который исказит истинное положение и завысит среднюю цену реализации, так как не будет учтен тот факт, что большая доля в реализации приходится на позднюю капусту с более низкой ценой.

Иногда требуется определить среднюю величину, когда значения признака даются в виде дробных чисел, т. е. обратных целым числам (например, при изучении производительности труда через обратный его показатель, трудоемкость). В таких случаях целесообразно использовать формулу средней гармонической:

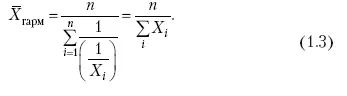
Так, среднее время, необходимое для изготовления единицы продукции, есть средняя гармоническая. Если Х 1= 1/4 часа, Х 2= 1/2 часа, Х 3= 1/3 часа, то средняя гармоническая этих чисел есть:

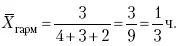
Для расчета средней величины из отношений двух одноименных показателей, например темпов роста, применяется средняя геометрическая, рассчитанная по формуле: