Леонид Букин - Статистика: учебное пособие

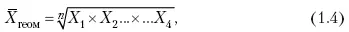
где Х 1× Х 2… × … Х 4– отношение двух одноименных величин, например цепных темпов роста; n – численность совокупности отношений темпов роста.

Рассмотренные средние величины обладают свойством маорантности:

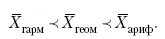
Пусть, например, имеем следующие значения Х (20; 40), тогда рассмотренные ранее виды средних величин будут равны:

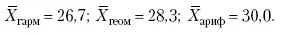
При изучении состава совокупности о типичном размере признака можно судить по так называемым структурным средним – моде и медиане.

Модой называется наиболее часто встречающееся значение признака в совокупности. В интервальных вариационных рядах сначала находят модальный интервал. В найденном модальном интервале мода рассчитывается по формуле:

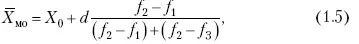
где Х 0– нижняя граница модального интервала; d – величина интервала; f 1, f 2, f 3 – частоты предмодального, модального и послемодаль-ного интервалов.

Значение моды в интервальном ряду довольно просто можно отыскать на основе графика. Для этого в самом высоком столбце гистограммы от границ двух смежных столбцов проводят две линии. Из точки пересечения этих линий опускают перпендикуляр на ось абсцисс. Значение признака на оси абсцисс и будет модой (рис. 2).

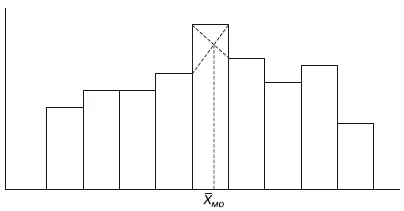
Рис. 2

Для решения практических задач наибольший интерес представляет обычно мода, выраженная в виде интервала, а не дискретным числом. Объясняется это назначением моды, которая должна выявить наиболее распространенные размеры явления.

Средняя – величина, типичная для всех единиц однородной совокупности. Мода – тоже типичная величина, но она определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Она имеет большое значение для решения некоторых задач, например для прогнозирования того, какие размеры обуви, одежды должны быть предназначены для массового производства, и т. д.

Медиана – значение признака, находящееся посредине ранжированного ряда. Она указывает на центр распределения единиц совокупности и делит ее на две равные части.

Медиана является лучшей характеристикой центральной тенденции, когда границы крайних интервалов открыты. Медиана является более приемлемой характеристикой уровня распределения и в том случае, если в ряду распределения имеются чрезмерно большие или чрезмерно малые значения, которые оказывают сильное влияние на среднюю величину, а на медиану – нет. Медиана, кроме того, обладает свойством линейного минимума: сумма абсолютных значений отклонений величины признака у всех единиц совокупности от медианы минимальная, т. е.

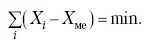
Это свойство имеет большое значение для решения некоторых практических задач – например, для расчета самого короткого из всех возможных расстояний для разных видов транспорта, для размещения станций техобслуживания таким образом, чтобы расстояние до всех обслуживаемых данной станцией машин было минимальным, и т. п.

При отыскании медианы сначала определяется ее порядковый номер в ряду распределения:

Далее, соответственно порядковому номеру, по накопленным частотам ряда находят саму медиану. В дискретном ряду – без всякого расчета, а в интервальном ряду, зная порядковый номер медианы, по накопленным частотам отыскивается медианный интервал, в котором путем простейшего приема интерполяции определяется уже значение медианы. Расчет медианы осуществляется по формуле:

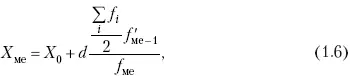
где Х 0 – нижняя граница медианного интервала; d – величина интервала; f _ 1– частота, накопленная до медианного интервала; f – частота медианного интервала.

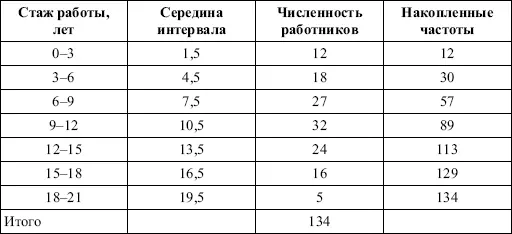
Рассчитаем среднюю величину, моду и медиану на примере интервального распределения. Данные приведены в табл. 2.

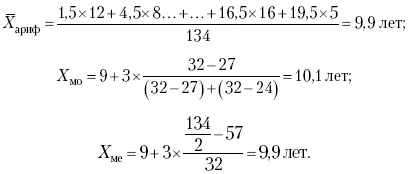
Таким образом, в качестве центра распределения могут быть использованы различные показатели: средняя величина, мода и медиана,

и каждая из этих характеристик имеет свои особенности. Так, для средней величины характерно то, что все отклонения от нее отдельных значений признака взаимно погашаются, т. е.

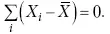
Для медианы характерно то, что сумма отклонений индивидуальных значений признака от нее (без учета знаков) является минимальной. Мода же характеризует наиболее часто встречающееся значение признака. Поэтому в зависимости от того, какая из особенностей интересует исследователя, и должна выбираться одна из рассмотренных характеристик. В отдельных случаях рассчитываются все характеристики.

Их сравнение и выявление соотношений между ними помогает выяснить особенности распределения того или иного вариационного ряда. Так, в симметричных рядах, как в нашем случае, все три характеристики (средняя, мода и медиана) примерно совпадают. Чем больше расхождение между модой и средней величиной, тем более асимметричен ряд. Установлено, что для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней арифметической:

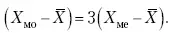
Это соотношение можно использовать для определения одного показателя по двум известным. Из этого следует, что сочетание моды, медианы и средней важно и для характеристики типа распределения.

Статистическое описание совокупности было бы неполным, если ограничиться лишь показателями центральной тенденции, т. е. средними величинами, модой и медианой, которые являются равнодействующими ряда изменяющихся значений признака. В одних случаях значение признака концентрируется возле некоторого центра очень тесно, в других случаях наблюдается значительное рассеивание, хотя средняя величина может быть одинаковой. В связи с этим средняя величина как показатель центральной тенденции не дает исчерпывающей характеристики изучаемой совокупности. Возникает необходимость изучения характера рассеивания признака. Хотя отклонения от средней и регулируются общими для всех единиц совокупности причинами, формирующими среднюю, но в то же время они обусловлены и индивидуальными причинами. Например, отклонения производительности труда отдельных рабочих, работающих в одной бригаде, а стало быть, находящихся в одинаковых условиях труда, вызваны не общими условиями и причинами, а индивидуальными обстоятельствами рабочих и их квалификацией, состоянием здоровья, настроением, сообразительностью и т. д. Поэтому изучение отклонений от средней их размеров и закономерности распределения представляет большой интерес для исследователя. Это важно прежде всего для оценки однородности совокупности, которую характеризует данная средняя величина, так как для качественно однородной совокупности характерна вариация в определенных границах. Стало быть, чем меньше вариация, тем качественно однороднее совокупность, тем типичнее и объективнее средняя величина, характеризующая ее.