Леонид Букин - Статистика: учебное пособие

Измерение вариации имеет большое значение и для изучения устойчивости изучаемых экономических явлений и процессов. Так, для сельского хозяйства очень важно не только получить среднюю урожайность сельскохозяйственных культур, но и обеспечить ее устойчивость во времени и пространстве, а для этого надо научиться рассчитывать показатели устойчивости, научиться измерять вариацию изучаемых явлений σ ≈ 1,25 а .

Для оценки вариации признака статистика знает и использует несколько показателей. Простейшим из них является размах вариации, рассчитываемый по формуле: X max– X min, т. е. как разность между максимальным и минимальным значением признака. Однако этот показатель далеко не совершенен, так как при его построении участвуют лишь крайние значения признака, которые могут быть случайными.

Более точно можно определить вариацию признака при помощи показателя, учитывающего отклонения всех значений признака от средней. Это так называемые абсолютные показатели: среднее линейное отклонение а и среднее квадратическое отклонение σ. Среднее линейное отклонение – это средняя арифметическая из абсолютных значений отклонений отдельных значений признака от средней величины. Но сумма отклонений от средней

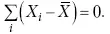
всегда равна нулю (одно из свойств средней величины), поэтому для расчета среднего линейного отклонения суммируют абсолютные отклонения без учета его знака:

Среднее квадратическое отклонение также может быть простое и взвешенное:

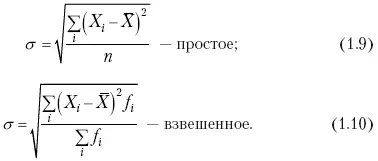
Среднее квадратическое отклонение является наиболее распространенным показателем вариации, оно несколько больше среднего линейного отклонения. Установлено, что в симметричных или умеренно асимметричных распределениях соотношение между ними можно записать в виде:

σ ≈ 1,25 а .

Следует иметь также в виду, что среднее линейное отклонение будет минимальным, если оно рассчитано от медианы, т. е.:

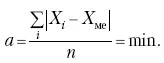
Среднее квадратическое отклонение минимально при вычислении его от средней арифметической, это же относится и к дисперсии, которая представляет собой квадрат среднего квадратического отклонения.

Дисперсия

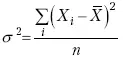
широко применяется в дисперсионном анализе, но не как мера вариации, так как ее размерность не соответствует размерности признака.

Содержание среднего квадратического отклонения то же, что и среднего линейного отклонения: т. е. чем меньше а и? тем однороднее совокупность, тем типичнее (объективнее) средняя величина, тем устойчивее явление и процесс.

Рассмотрим вычисление среднего линейного и среднего квадрати-ческого отклонения на примере данных, приведенных в табл. 3.

Таблица 3.

Анализ времени обработки деталей рабочими двух бригад

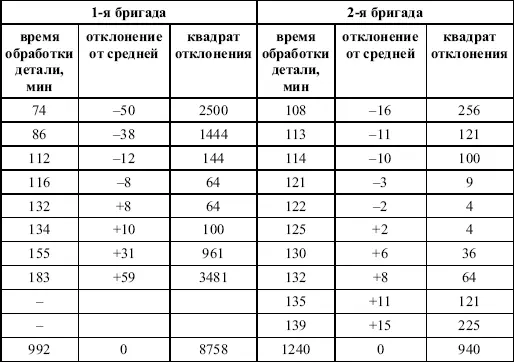
Средняя величина времени обработки детали составляет в обеих бригадах 124 мин. Для первой бригады Х 1 =992/8 = 124ми н. и для второй – Х 2 = 1240/10 = 124 мин.

Медианные значения также одинаковы в обеих бригадах. Так, для первой бригады Хме = (116+132)/2 = 124 мин. Для второй бригады – Хме = (122+126)/2 + 124 мин

Модальные значения в данном случае не могут быть определены, так как каждое из значений признаков не повторяется.

Исходя из полученных результатов, можно сделать вывод, что обе совокупности характеризуются одинаковыми показателями центра распределения, но они могут отличаться по характеру рассеяния отдельных значений признака вокруг этих центров.

Для характеристики рассеяния рассчитаем среднее линейное отклонение. Для первой бригады:

Сопоставление среднего линейного и среднего квадратического отклонений говорит о том, что вариации времени обработки деталей в первой бригаде значительно выше, чем во второй бригаде.

Следует также отметить, что среднее квадратическое отклонение в обоих случаях несколько больше, чем среднее линейное отклонение:

σ 1= 1,22а 1;

σ 2= 1,20а 2.

Это говорит о том, что мы имеем дело с умеренно асимметричным распределением.

Рассмотренные показатели вариации (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение) дают возможность сравнить степень однородности нескольких совокупностей, но в отношении лишь одного признака, поскольку это именованные величины, имеющие единицы измерения те же, что и сам признак.

Однако часто исследователю приходится сравнивать вариации различных признаков, а стало быть, эти показатели вариации не могут быть использованы.

Для характеристики вариации различных признаков рассчитывают относительные показатели вариации, приведенные к одному основанию, т. е. выраженные в процентах (доли размаха вариации, среднего линейного отклонения и среднего квадратического отклонения) от средней величины изучаемого признака.

Это так называемые коэффициент осцилляции, относительное отклонение и коэффициент вариации.

Коэффициент осцилляции рассчитывается по формуле:

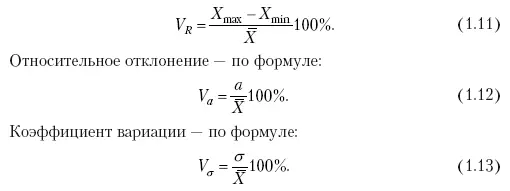
В нашем примере эти показатели составляют:

Все рассчитанные относительные показатели вариации свидетельствуют также о более сильной вариации времени обработки деталей рабочими первой бригады по сравнению со второй, где среднее время обработки является более объективной, более типичной характеристикой работы данной бригады в целом, т. е. вторая бригада как совокупность более однородна.

Относительные показатели вариации, как уже было отмечено, позволяют сравнивать степень вариации признаков, имеющих одинаковые единицы измерения, но разные уровни средних. Например, урожайность зерновых культур и картофеля хотя и имеют одинаковые единицы измерения, но по абсолютным показателям вариации этих признаков сравнивать было бы неправильно, так как сами уровни урожайности зерновых и картофеля резко отличаются. Так, например, в регионе среднеквадратическое отклонение составило: по урожайности ржи – 5 центнеров с гектара (ц/га) и по урожайности картофеля – 20 ц/га, а сама урожайность ржи составила 25 ц/га, а картофеля – 200 ц/га. Коэффициент же вариации соответственно равен: