Журнал «Знание-сила» - Знание-сила, 1997 № 08 (842)

не только способности быстро «пережевывать» числа и получать значения требуемых данных, но и наглядно представлять гигантские массивы числовой информации. Суперкомпьютеры десятилетней давности, такие сверхмощные, как «Конвекс», «Сайбер-205» и тогдашний лидер лидеров — «Крей», уже были отменно приспособлены для перемалывания чисел (если строго — для арифметических операций над вещественными числами), но плохо преобразовывали числовые массивы в более понятные образы — с цветом, сложными геометрическими формами, прозрачностью или отражательными свойствами, хитрым распределением освещенности. Набор таких образов в трехмерном пространстве с пространственными соотношениями между ними образует сцену, характеризующуюся глубиной, а если добавить зависимость от времени — динамическими свойствами. Получение подобной сцены и есть компьютерная визуализация данных (visual computing) Например, медицинская томография — классическая задача компьютерной визуализации.

Прообразом процедуры визуализации может служить построение графика функции, типичная задачка школьной математики. При этом разные ученики строят 1рафнки по- разному: одни попросту подставляют в исходное алгебраическое выражение много произвольно взятых числовых значений (построение «по точкам»), другие используют соображения, близкие к геометрическим,— свойства симметрии, минимумы и максимумы, точки перегиба, пересечения с осями, асимптотики, наконец, понимание поведения функции «в целом».

Первый способ при выборе подставляемых значений аргумента не произвольно, а в виде периодической последовательности — ее в электронике называют растром — служит прообразом растровой графики со всеми ее достоинствами и недостатками (например, «эффектом лестницы» при построении непрерывной функции, когда плавная кривая заменяется «ступенчатой»). Второй способ отражает принципы геометрического моделирования.

Заметим, что уже одномерная визуализация обладает изрядной эвристической, прогностической силой, о чем свидетельствует пример «теории катастроф». Лет пятнадцать — двадцать назад эта дисциплина вдруг стала исключительно модной, своими претензиями на универсальность напоминая астрологию. Если встать на позиции математического пуризма, то «теории катастроф» просто не существует — ее результаты укладываются в известную, появившуюся задолго до нее теорию особенностей гладких отображений. Однако про последнюю никто, кроме профессиональных математиков, не вспоминал, а вот книжки по теории катастроф выходили массовыми тиражами и раскупались, как детективные романы.

На вопрос: почему так?, один из ответов состоит, видимо, в том, что в теории катастроф все явления представлены графически. Причем те, что отражают предсказуемые, постепенные события, изображены плавной частью кривой (или поверхности), а внезапные — катаклизмы, срывы, катастрофы — соответствуют ломке, падению, обрыву той же кривой или поверхности. При этом важно то, что у нас возникает понимание: резкое изменение — катастрофа — как бы зреет при плавном развитии событий и в конце концов становится неотвратимой. Такой срыв накапливающейся «революционной ситуации» напоминает прыжок лыжника с трамплина. Книжки по теории катастроф изобилуют картинками — вещь для чистой математики непривычная, отдающая обывательской нестрогостью. Но именно благодаря картинкам теория катастроф помогает жить и работать многим нематематикам, вынужденным анализировать довольно сложные динамические системы, например, в экономике.

В современной науке существует несколько методов определения пространственных координат и визуализации трехмерных объектов: рентгеновская, звуковая, сейсмическая, магниторезонансная (ЯМР, по- английски MRI) и позитронная (РЕТ) томография; измерения с помощью радара, лидара и сонара, а также голографическая интерферометрия. Недавно были развиты лазерные спектроскопические методики (в частности, нелинейнооптические) трехмерной визуализации скрытых объектов, особенно эффективные в медицинской интроскопии.

1

2

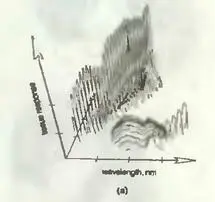
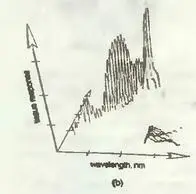
На этой странице приведено изображение, полученное в результате оптической биопсии, неинвазивного, то есть не травмирующего, в отличие от обычной биопсии, исследования тканей при подозрении на онкологическое заболевание.

Когда подозрительный участок или орган освещается лазерным импульсом, спектральный отклик — своего рода оптическая подпись — раковой ткани (№ 2) заметно отличается от отклика нормальной ткани (№ 1).

Наиболее известным сегодня примером трехмерной визуализации может служить компьютерная томография.

Еще совсем недавно единственным способом неинвазивно проникать в человеческое тело и разглядывать многие из внутренних органов было использование рентгеновских лучей.

4

5

Однако обычные методы, даже при очень хорошей рентгеновской трубке (источнике) и сверхчувствительной фотопленке (приемнике), дают нечеткое и сильно «зашумленное» изображение, к тому же только двумерное, так что правильно его интерпретировать — отдельная наука.

В отличие от традиционных рентгеновских методов томография представляет собой объемную реконструкцию внутренних органов на основе числовых данных, полученных как характеристики физических свойств тканей. Средства машинной графики позволяют показать, например, трехмерное изображение плода, полученное на ЯМР- томографе. Врач может рассматривать мельчайшие детали, как угодно преобразовывать изображение, его можно также легко сжимать, архивировать, передавать по каналам связи для участии в телеконсилиумах и т. л.

3

Да и самим исследователям, судя по всему, графическая методология теории катастроф позволяет «думать карандашом».

Однако все так легко и понятно (а в эмоциональном смысле — приятно) только в одномерном случае. Как только задача становится многомерной, сразу возникают трудности, часто непреодолимые. Простой пример: геометрические свойства плоской кривой вполне характеризуются ее кривизной, но если линия выходит из плоскости и становится пространственной, то кривизны для ее описания уже недостаточно и необходима еще одна величина, называемая кручением. Для поверхностей все усложняется еще больше, что, собственно, и послужило поводом для создания наиболее мощного в современной науке аппарата новой геометрии.