Борис Ломов - Психическая регуляция деятельности. Избранные труды

Такое предположение тем более кажется допустимым, что частоты микроколебаний глаз (тремор) достигают 100 град/сек, а это требует для создания автоколебательного режима минимальных инерционных задержек, т. е. минимально допустимых пространственных связей с мышцей. Кроме того, действие такого механизма может объяснить возникновение микросаккад, часто повторяющихся с интервалом менее 50 мсек, что значительно меньше времени обычной фиксации.

Нами была предпринята попытка экспериментально проверить, существует ли регулирование по производной. В экспериментах наблюдателю преддагалось следить за точкой, перемещающейся по определенному закону из центра экрана на некоторый угол. Скорость движения точки была подобрана так, чтобы это движение осуществлялось за время, меньшее латентного периода зрительной системы: к началу движения глаза точка останавливалась и занимала заданное положение. В этих условиях можно было ожидать три возможных типа переходной характеристики работы зрительной системы (в зависимости от ее функциональной схемы). В том случае, если система работает по жесткой программе, когда заранее задаются характеристики движения глаза (скорость, амплитуда), система не смогла бы выйти в нужное положение без дополнительной коррекции, поскольку положение стимула изменялось вплоть до начала скачка, а значит, и информация о конечном его положении во время латентного периода не могла бы быть обработана. Для случая регулирования только по положению характеристика переходного процесса должна была бы соответствовать входному сигналу, а процесс регулирования по времени не отличался бы от времени действия входного сигнала (порядка 250 мсек) . Как показали эксперименты, скорость начальной фазы поворота глаза значительно больше скорости движения стимула и приближается к скорости скачка: во второй половине движения он, наоборот, оказывается замедленным. Общее время движения глаза в 2–2,5 раза меньше, чем время предъявления стимула.

Таким образом, экспериментальные данные оказались более всего соответствующими третьему типу переходной характеристики, т. е. переходный процесс соответствует системе, имеющей регулирование по производной (по скорости).

Эти данные свидетельствуют также и о том, что время между моментом предъявления стимула и началом движения глаза (латентный период) идет не на обработку данных о появившемся стимуле (определения его координат) и составление двигательной программы, а представляет «чистое запаздывание» системы регулирования, т. е. время, необходимое для проведения сигнала по контуру регулирования. Заметим, что «чистое запаздывание» не вносит каких-либо изменений в характер переходного процесса (переходный процесс определяется инерционностью системы), а лишь смещает его по времени. Этот факт необходимо учитывать при определении амплитудно-частотных и фазово-частотных характеристик системы. Структурная схема системы с учетом «чистого» запаздывания показана на рисунке 1.11, а уравнение звена запаздывания имеет вид

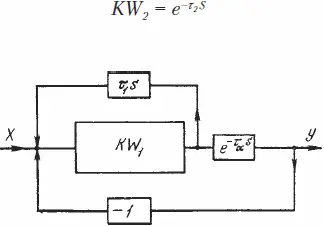
Рис. 1.11. Структурная схема следящей системы с цепью «чистого» запаздывания

Поскольку чистая задержка не вносит искажений в вид переходного процесса, в установившемся режиме при синусоидальном входном сигнале реакция системы будет определяться временем нарастания t 1(см. рисунок 1.8).

Ориентировочно можно принять, что f ср= 0,45/t = 0,45/0,05 = 9 гц. Однако по экспериментальным данным верхние частоты, при которых еще осуществляется достаточно хорошее отслеживание стимула, составляют 1–2 гц [150]. При больших частотах отслеживание прерывается скачками: система оказывается в неустойчивом режиме. Это явление связано с тем, что фазовое запаздывание оказывается близким к я, что и нарушает устойчивость системы. На рисунке 1.12 показано, что при чистой задержке системы в 250 мсек выходной сигнал частотой 2 гц оказывается в противофазе с управляющим сигналом, т. е. по цепи отрицательной обратной связи он приходит к входу системы с тем же знаком, что и входной, увеличивая рассогласование. Таким образом, частотные свойства апериодического звена второго порядка ограничивают полосу пропускаемых системой частот, а фазовые задержки определяются «чистым запаздыванием». Вместе с тем, изменяя коэффициент усиления системы, можно в определенных пределах изменять частоту, при которой система будет еще устойчива. Обычно частотный анализ систем проводится с помощью логарифмических амплитудно-и фазово-частотных характеристик. Об устойчивости системы с обратной связью можно судить по логарифмическим амплитудно– и фазово-частотным характеристикам разомкнутой системы. Такие характеристики представляют собой графики, на которых в логарифмическом масштабе отложены по оси абсцисс частота 1gv, а по оси ординат – амплитуды выходного сигнала 1g А – для амплитудно-частотной характеристики и сдвиг фазы выходного сигнала j по отношению к входному для фазовой характеристики. Соответствующие характеристики рассматриваемой системы при разомкнутой обратной связи представлены на рисунке 1.13. Известно, что замкнутая система автоматического регулирования устойчива, если фазово-частотная характеристика разомкнутой системы пересечет линию я в области отрицательных значений амплитудно-частотной характеристики. Представленные на рисунке 1.13 характеристики построены для коэффициента усиления системы К = 1. Увеличение коэффициента усиления никак не сказывается на форме и положении логарифмической фазово-частотной характеристики. Амплитудно-частотная характеристика при увеличении коэффициента усиления смещается вверх на величину, пропорциональную К, а при уменьшении этого коэффициента – вниз.

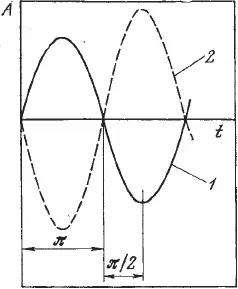
Рис. 1.12. Схема фазового запаздывания сигнала в системе с обратной связью 1 – сигнал обратной связи; 2 – входной сигнал

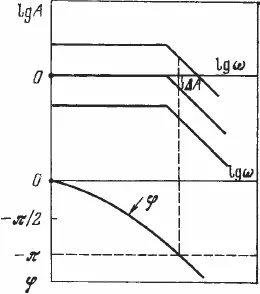
Рис. 1.13. Логарифмические амплитудно-частотные и фазово-частотные характеристики апериодической системы второго порядка при различных коэффициентах усиления ( 1–4 )

Такое отрицательное значение логарифмической амплитудно-частотной характеристики, при котором фазово-частотная характеристика принимает значение я, называется запасом устойчивости системы по амплитуде D А. Таким образом, рисунок 1.13 показывает, что увеличение К уменьшает запас устойчивости системы и даже может сделать ее неустойчивой. Уменьшение К, наоборот, увеличивает запас устойчивости системы. Уменьшение запаса устойчивости означает срывы; возникновение неустойчивых колебаний будет наблюдаться в работе системы при частотах, меньших, чем те, на которых она теряла устойчивость, когда К=1.