Питер Макоуэн - Вычислительное мышление: Метод решения сложных задач

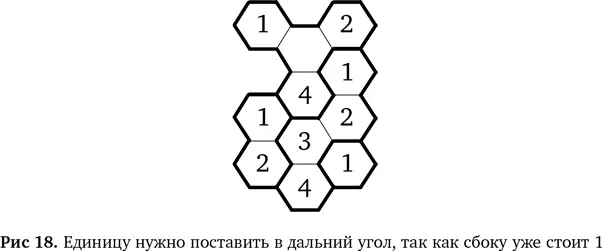
Соответственно, в последний шестиугольник надо поставить 3, поскольку в этой области должны стоять числа 1–4 и недостает только 3. Решение целиком показано на рис. 19.

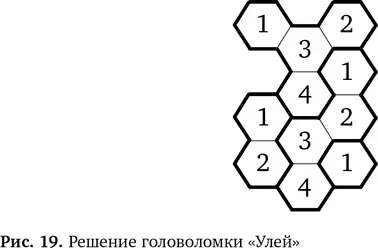
Мы разгадали головоломку. И сделали это, исходя из двух правил и исходных данных — известных чисел. Основываясь на них, мы многократно выявляли новые факты в этой головоломке. Мы прибегли к особому виду логических рассуждений, называемому дедукцией,который позволяет с помощью известных фактов и правил мироустройства (в данном случае — правил головоломки) получать новые факты. Считается, что именно так Шерлок Холмс творил свои детективные чудеса. Он подмечал разные детали в людях и ситуациях, а потом с помощью дедукции выводил новые факты, которые являлись следствием этих деталей. Чем больше фактов он узнавал, тем дальше мог продвинуться в дедукции, что и позволяло в конечном итоге раскрывать преступления. Ученые-информатики и математики используют похожий метод. Хорошие программисты обращаются именно к дедукции, чтобы убедиться в бесперебойной работе своих программ.

До сих пор мы выводили факты непосредственно из двух правил. Но решив много головоломок и обретя опыт, мы берем на вооружение другой подход — используем естественные навыки вычислительного мышления, например сопоставление с образцомиз ранее встречавшихся ситуаций. Этот метод позволяет решать головоломки быстрее и тратить меньше времени на их обдумывание. Следующий шаг — обобщение, то есть для поиска образцов мы расширяем круг ситуаций, а не возвращаемся к уже известным. При наличии опыта мы начинаем создавать новые, ускоренные и универсальные правила, которые позволяют вести логические рассуждения на более высоком уровне. Это становится возможным благодаря использованию логического мышленияне с целью решить конкретную головоломку, как мы делали до сих пор, но с целью создать новые правила. При этом мы уверены, что эти новые правила гарантированно выведены из основных. Давайте посмотрим, о чем идет речь, на некоторых примерах.

Вернемся к решению предыдущей головоломки. Мы выяснили, что, если в области содержится только один шестиугольник, в нем должна стоять 1. Это следует непосредственно из первого правила. Осознав, что нет необходимости снова это обдумывать, мы можем из начального правила вывести новое.

3. ЕСЛИв области есть только один шестиугольник, ТОв нем может стоять только 1.

Чтобы наглядно представить это правило и не ограничиваться словами, мы набросаем схему (рис. 20). Стрелка показывает, какие изменения мы вносим в улей. Слева изображена позиция сопоставления с образцом, а справа — вносимые изменения, если найдем образец. Подобные правила называются порождающими правилами, правилами логического выводаили правилами подстановки.Наше правило в виде схемы показывает, что если мы найдем пустой участок в один шестиугольник, то можем преобразовать его в шестиугольник с 1.

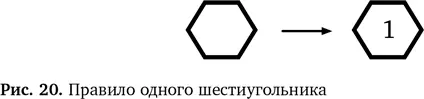
Теперь можно применять это правило, даже не задумываясь, почему оно работает. Наше логическое мышление теперь оперирует на более высоком уровне, по крайней мере в такой простой ситуации.

Теперь выведем еще одно новое правило для областей, состоящих из двух шестиугольников. Мы видели, что если есть область из двух шестиугольников и в одном стоит 2, то во второй нужно поставить 1 (рис. 21).

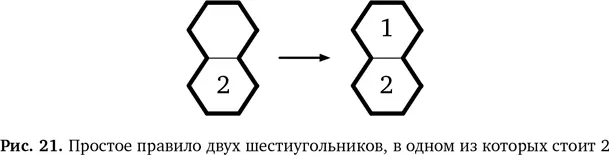
Мы вправе рассматривать это как обобщенноеправило из конкретного примера нашей головоломки. Не важно, в каком шестиугольнике стоит 2, — логика не меняется. Даже если картинку перевернуть, правило останется прежним. Это правило применимо и к шестиугольникам, соприкасающимся по диагонали в любом направлении. Но обобщение можно продолжить. По той же логике, если в области из двух шестиугольников в одном уже стоит 1, в другой нужно поставить 2. Это показано на рис. 22.

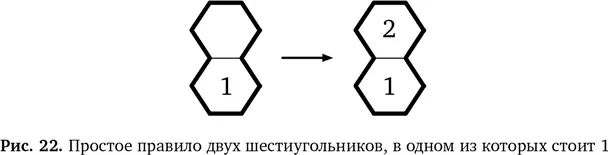
Объединив два эти отдельные правила, мы получаем полное обобщенное правило:

4. ЕСЛИодин шестиугольник в области из двух содержит 1 или 2,

ТОв другом шестиугольнике будет второе число из этих двух.

Правило можно представить в виде схемы, где xбудет обозначать любое число (точно так же, как математики используют xи yдля обозначения переменных в алгебре).

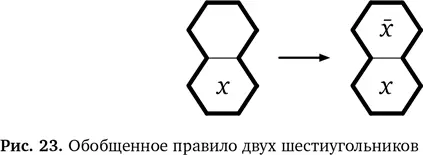
В одном случае xзаменяет 1, а в другом — 2, но замена остается неизменной в рамках одного примера. Схема правила приведена на рис. 23. На схеме xобозначает другое число. То есть если x — это 1, то x —это 2 и если x — это 2, то x —1. Это правило подходит для области из двух шестиугольников, повернутой в любую сторону, и не важно, какое число стоит наверху, а какое — внизу. Схема превращается в одно из изначальных правил (и их схем), если заменить xна 1 или 2. Так мы начали изобретать своего рода математические обозначения, которые используются с той же целью, что и символы в математике. Они дают возможность говорить о вещах с большой точностью, и это важно, так как по мере усложнения правил надо стараться избегать возможных ошибок.

Вместо того чтобы выводить новые факты из заданных фактов, используя исходные правила решения головоломки, мы теперь выводим новые, «более крупные» правила с учетом исходных. Это называется производные правила логического вывода.Когда мы видим ситуацию, соответствующую образцу из какого-то нового правила, мы уже не думаем, почему оно верно, а просто применяем его. Мы абстрагировалисьот обоснования, стоящего за правилом.

Давайте рассмотрим последний пример создания более общего правила на базе нашего для решения простой головоломки. Оказывается, он весьма полезен. Мы поняли, куда поставить 1 в области из четырех шестиугольников в нижнем углу. Это было возможно, потому что в прилегающей области уже стояла 1, устроившаяся в углу, как показано на рис. 24.

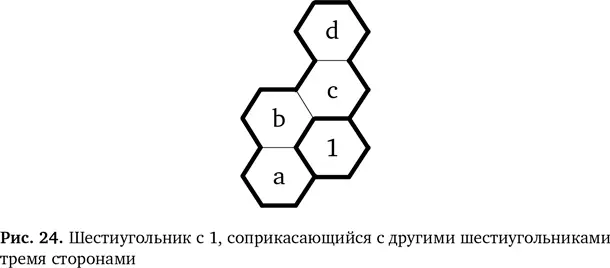
Единицу нужно поставить в позицию a, b, c или d (рис. 24). Однако в соответствии со вторым правилом головоломки рядом не должна находится ячейка с 1. Значит, позиции b и с исключаются. Остается только позиция d, и только туда получается поставить 1. Мы можем изобразить этот этап в виде схемы для правила замены (рис. 25).