Питер Макоуэн - Вычислительное мышление: Метод решения сложных задач

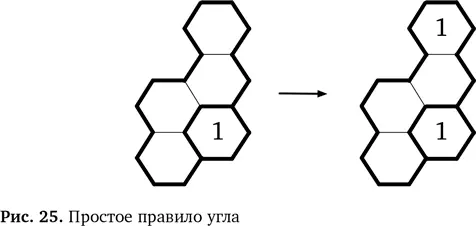
Конечно, в любых пустых шестиугольниках уже могут стоять числа, но правило остается справедливым — это еще один способ обобщитьнаше новое правило. Кроме того, число, которое мы используем при сопоставлении с образцом, необязательно должно быть 1. Это может быть любое другое число в рамках достаточно большой области. Если мы опять поставим xна место любого возможного числа, то наше правило становится обобщенным вариантом (рис. 26).

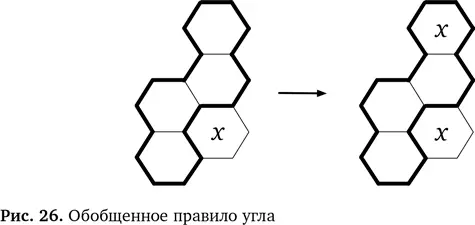
Мы даже можем продолжить обобщение нашего правила. Область, которую мы заполняем, не должна иметь заданную форму. Следующий шестиугольник может стоять в любой позиции у дальнего края более крупной области — везде, где он связан с угловым шестиугольником, но не касается его. В варианте правила угла на рис. 27 мы использовали вопросительные знаки, которые показывают возможные положения этого шестиугольника.

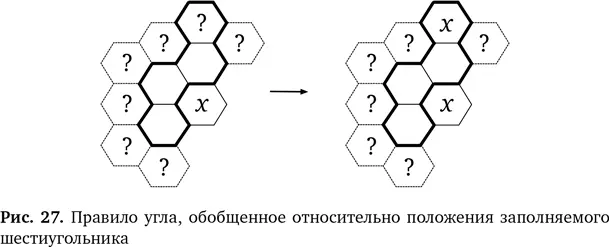
Получаем обобщенное правило:

5. ЕСЛИшестиугольник соседствует с областью из четырех шестиугольников и только три из четырех соприкасаются с ним, ТОв четвертом будет стоять то же число, что и в указанном вначале шестиугольнике.

Как и в предыдущих случаях, правило применимо при любом положении схемы — перевернутом, горизонтальном, под углом или отраженном. Возможно, вы найдете больше способов обобщитьправило.

Итак, сейчас у вас есть вышеприведенное общее правило. Если в головоломке вы увидите ситуацию, сопоставимую с образцом, правило можно применить. Вставьте пропущенное число, которое соответствует x.

Большинство при решении головоломок не записывают правила, которые они выводят и используют. Люди просто запоминают сработавший метод и, особенно не задумываясь, по возможности применяют его. Однако специалисты по информатике любят записывать такое. Зачем это делать? Примерно по тем же причинам, что и записывать алгоритмы. Их можно использовать, например, чтобы научить других разгадывать головоломки (как это сделали мы), и тогда им не придется проходить весь этот путь с самого начала. Правила можно использовать, чтобы научить компьютер разгадывать головоломки. Кроме того, это делается ради точности. Довольно часто возникают ложные воспоминания о сработавших правилах, или мы можем выучить их, не до конца уловив детали. В любом случае в результате правило может использоваться неверно или в новой ситуации, которой оно не очень соответствует. Если записать все точно, то мы избежим такого рода ошибок.

Но здесь уже не получится использовать рисунки, как сейчас. В информатике для записи правил используют математические обозначения ( формальную логику). Языки для описания этой логики немного похожи на языки программирования, но при этом они очень гибкие. Их большое преимущество состоит в том, что их легко обработать на компьютере, и затем на их основе компьютер может строить логические рассуждения. Так логика становится основой для компьютерных программ, которые позволяют решать головоломки.

Многие системы искусственного интеллекта основаны на идее использования порождающего правила.Вместо того чтобы рисовать схемы, мы пишем правила в следующем виде:

ЕСЛИ <���какая-то ситуация > ТО <���действие, которое надо выполнить >

Список таких правил представляет собой программу. Если правило работает, то компьютер может выполнить действие. Если совпадают несколько правил, он выбирает любое, и все повторяется снова и снова. Такой подход обеспечивает новую парадигму для создания программ и позволяет совершенно по-другому увидеть их сущность. Это не просто последовательность команд для выполнения, о которой мы говорили до сего момента, а новый тип мышления.

Все лучше осваивая искусство решения головоломок, мы не просто используем логическое мышление, а сопоставляем с образцомтекущую ситуацию, чтобы узнать, какое правило нужно применить. Программа, основанная на порождающих правилах, делает похожее сопоставление с образцом. Это простое вычислительное мышление.

Когда мы записываем правила для создания программы, обобщениеидет рука об руку с абстрагированием.Мы скрываем подробности, касающиеся других частей головоломки, чтобы было легче продумывать, как шире обобщить правила. На схеме, иллюстрирующей наше последнее правило, мы использовали несколько абстракций, чтобы описать, как осуществлять сопоставление с образцом.Например, переменная x— это абстракция.Мы абстрагируемся от конкретного числа (то есть опускаем подробности) — правило применимо независимо от числа. Кроме того, мы используем знак вопроса в качестве другой переменной, чтобы абстрагироваться от конкретного положения четвертого шестиугольника в нашем представлении правила. Подобным образом мы абстрагируемся от ориентации схемы — ее можно как угодно вращать или отражать, но она будет соответствовать решаемой головоломке.

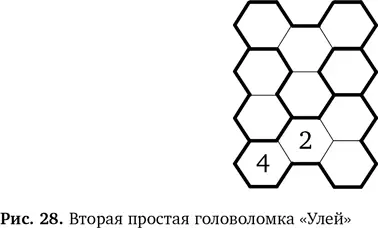
На рис. 28 представлена новая головоломка. Посмотрите, можно ли использовать приведенные выше правила для ее решения. В процессе разгадывания вы найдете новые правила. Если ни одно из выведенных ранее правил не подойдет, возможно, стоит вернуться к исходным. Помните, что по второму правилу два одинаковых числа не могут находиться рядом. Ответ приведен в конце главы.

На рис. 29 показана еще одна головоломка, значительно больше и сложнее. Решая ее, выводите новые правила — те, что пригодятся при решении этой головоломки, и те, что могут пригодиться в будущем.

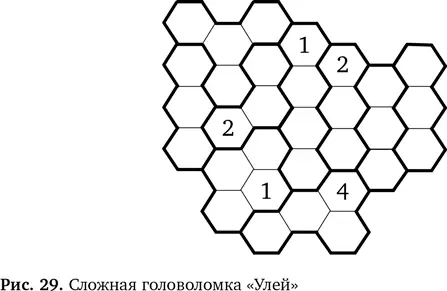
СОВЕТ. Когда будете искать новое правило, обратите внимание на то, что происходит, когда области из трех шестиугольников граничат друг с другом.

Какую роль логическое мышлениеиграет в информатике? Центральную. Работа компьютеров основана на логике, а значит, чтобы программировать их, давать им указания, нужно мыслить логически. В противном случае вы с большой вероятностью ошибетесь.

Логическое мышление— один из ключевых компонентов вычислительного мышления, которое проходит через все его аспекты, и не важно, какая стоит задача — создавать алгоритмы или оценивать их. Программистам необходимо мыслить логически, когда они разрабатывают новую программу, переделывают уже существующую под новые задачи, ищут дефекты программного кода или проводят иную оценку.