Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

1) проверка временного ряда на стационарность;

2) идентификация порядка модели и оценивание неизвестных параметров;

3) прогноз.

Применение модели АРПСС предполагает обязательную стационарность исследуемого ряда, поэтому на первом этапе данное предположение проверяется с помощью автокорреляционной и частной автокорреляционной функций ряда остатков. Остатки представляют собой разности наблюдаемого временного ряда и значений, вычисленных с помощью модели.

Устранить нестационарность временного ряда можно с помощью метода разностных операторов.

Разностным оператором первого порядка называется замена исходного уровня временного ряда разностями первого порядка:

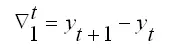
Разностные операторы первого порядка позволяет исключить линейные тренды.

Разностные операторы второго порядка позволяют исключить параболические тренды.

Сезонные разностные операторы предназначены для исключения 12-ти или 4-х периодичной сезонности:

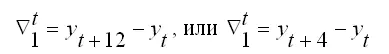
Если модель содержит и трендовую, и сезонную компоненты, то необходимо применять оба оператора.

На втором этапе необходимо решить, сколько параметров авторегрессии и скользящего среднего должно войти в модель.

В процессе оценивания порядка модели авторегрессии и проинтегрированного скользящего среднего применяется квазиньютоновский алгоритм максимизации правдоподобия наблюдения значений ряда по значениям параметров. При этом минимизируется (условная) сумма квадратов остатков модели. Для оценки значимости параметров используется t-статистика Стьюдента. Если значения вычисляемой t-статистики не значимы, соответствующие параметры в большинстве случаев удаляются из модели без ущерба подгонки.

Полученные оценки параметров используются на последнем этапе для того, чтобы вычислить новые значения ряда и построить доверительный интервал для прогноза.

Оценкой точности прогноза, сделанного на основе модели авторегрессии и проинтегрированного скользящего среднего является среднеквадратическая ошибка (mean squar e ), вычисляемая по формуле:

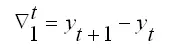
Чем меньше данный показатель, тем точнее прогноз.

Модель авторегрессии и проинтегрированного скользящего среднего считается адекватной исходным данным, если остатки модели являются некоррелированными нормально распределёнными случайными величинами.

Основными показателями качества модели авторегрессии и проинтегрированного скользящего среднего являются критерий Акайка и байесовский критерий Шварца. Данные критерии аналогичны критерию максимума скорректированного множественного коэффициента детерминации R2 или минимума дисперсии случайной ошибки модели G2 .

Информационный критерий Акайка (Akaike information criterion – AIC) используется для выбора наилучшей модели для временного ряда yt из некоторого множества моделей.

Предположим, что с помощью метода максимального правдоподобия была получена оценка

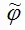
вектора неизвестных параметров модели φ . Обозначим через

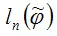
максимальное значение логарифмической функции правдоподобия эконометрической модели.

Тогда критерий Акайка можно будет представить в виде:

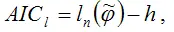
где h – размерность вектора неизвестных параметров модели φ.

Для линейной или нелинейной модели регрессии, включающей только одно уравнение, критерий Акайка может быть преобразован к виду:

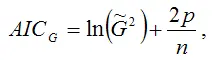
где n – объём выборочной совокупности;

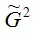
– оценка максимального правдоподобия дисперсии остатков et модели регрессии.

Оба варианта критерия Акайка дают одинаковый результат, но в первом случае выбирается модель с наибольшим значением критерия, а во втором случае – с наименьшим значением критерия.

Байесовский критерий Шварца (Schwarz Bayesian criterion – SBC) также используется для выбора наилучшей модели временного ряда из некоторого множества моделей.

Байесовский критерий Шварца для временных рядов можно представить в виде:

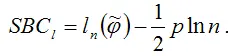
Байесовский критерий Шварца для моделей регрессии можно представить в виде:

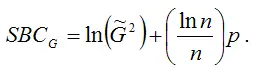
По первому варианту расчёта критерия Байесовского критерий Шварца SBC выбирается та модель, для которой значение SBCt является наибольшим. При втором варианте выбирается та модель, для которой значение SBCG является наименьшим.

При проверке качества моделей результаты критериев Акайка и Шварца могут быть различны.

Общий критерий множителей Лагранжа (LM-test) применяется для проверки качества модели авторегрессии и проинтегрированного скользящего среднего с помощью автокорреляции остатков. С помощью данного критерия можно обнаружить в остатках регрессии автокорреляцию более высоких порядков, чем первый, но при этом необходимо, чтобы выборочная совокупность была достаточно велика.

Предположим, что на основании собранных данных была построена модель регрессии вида:

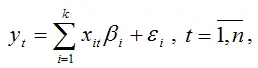
где εt – случайная ошибка модели:

εt=ρ1εt–1+ρ2εt–2+…+ρpεt-p+ut;

ρ – коэффициент автокорреляции порядка (1…ρ );

ut – нормально распределённая случайная величина с нулевым математическим ожиданием и дисперсией G2: ut ~N(0,G2).

Данная модель регрессии может в качестве факторных переменных включать лаговые значения зависимой переменной. Поэтому необходимо проверить основную гипотезу H 0 о незначимости коэффициентов автокорреляции:

H0:ρ1=ρ2=…=ρp=0.

Альтернативная гипотеза формулируется как утверждение о значимости коэффициентов автокорреляции: