Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике
- Название:Ответы на экзаменационные билеты по эконометрике
- Автор:
- Жанр:
- Издательство:Литагент «Ай Пи Эр Медиа»db29584e-e655-102b-ad6d-529b169bc60e
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике краткое содержание
Настоящее издание представляет собой учебное пособие и подготовлено в соответствии с государственным образовательным стандартом. Пособие составлено в виде ответов на экзаменационные билеты по дисциплине «Эконометрика».
Данное издание написано доступным языком и содержит всю необходимую информацию, достаточную для ответа на экзамене по данной дисциплине и успешной его сдачи.
Настоящие пособие предназначено для студентов высших и средних специальных учебных заведений.
Ответы на экзаменационные билеты по эконометрике - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Метод цензурирования переменных или наблюдений впервые возник в биологических и медицинских исследованиях. На современном этапе развития науки метод цензурирования используется в таких областях, как социология, демография и т. д. В частности в экономических исследованиях с помощью метода цензурирования анализируется время «выживания» новых предприятий или новой продукции, поступившей на рынок.
В зависимости от направления процесса цензурирования результативной переменной, выделяют правое и левое цензурирование.
Правым цензурированием результативной переменнойназывается процесс цензурирования, который характеризуется двумя отличительными чертами:
1) известна точка начала момента цензурирования;
2) известна точка окончания момента цензурирования.
Например, осуществляется проверка 100 предприятий, производящих однотипную продукцию, по определённым параметрам. При этом известны начало и конец проведения проверки.
Левое цензурирование не удовлетворяет вышеуказанным чертам, и применяется в биомедицинских исследованиях.
Однократным цензурированиеназывается цензурирование, которое наступает в один определённый момент времени.
Например, осуществляется проверка 100 предприятий, производящих однотипную продукцию. Если процесс проверки завершится спустя фиксированный отрезок времени, то использовалось однократное цензурирование, а исследуемые данные были цензурированы один раз.
Многократным цензурированиемназывается цензурирование, которое наступает в различные моменты времени.
Многократное цензурирование используется в биомедицинских исследованиях.
Цензурированием I типаназывается цензурирование, которое применяется в тех ситуациях, когда процесс тестирования завершается в заранее известный момент времени.
Например, при проверке 100 предприятий, производящих однотипную продукцию, процесс заканчивается через фиксированный отрезок времени. В этом случае количество предприятий, не прошедших проверку по установленным критериям, является случайной величиной, а время эксперимента – величиной заранее известной.
Цензурированием II типаназывается цензурирование, которое применяется в тех ситуациях, когда процесс тестирования завершается при достижении заданных критериев.
Например, при проверке 100 предприятий процесс тестирования будет закончен тогда, когда 25 предприятий не будут удовлетворять заданным критериям. В данном случае число забракованных элементов известно, а время эксперимента является случайной величиной.
Общий вид линейной модели регрессии с цензурированной результативной переменной:

При цензурировании результативной переменной пользуются методом усечения:
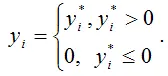
Оценки неизвестных коэффициентов модели регрессии с цензурированными переменными определяются с помощью метода максимума правдоподобия. В данной ситуации минимизируется логарифм функционала максимального правдоподобия вида:
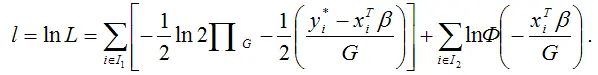
Если дифференцировать данный функционал по вектору неизвестных коэффициентов, то результатом будут оценки максимального правдоподобия
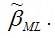
Однако существует вероятность того, что данные оценки не будут удовлетворять свойству несмещённости.
Смещение оценок максимального правдоподобия устраняется путём изменения функционала максимального правдоподобия и приведения его к виду:
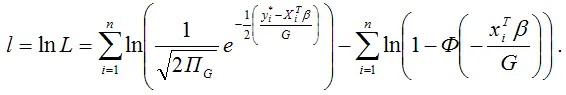
87. Системы эконометрических уравнений
Если экономический процесс не поддаётся описанию посредством одной модели регрессии, то в подобных ситуациях прибегают к построению нескольких эконометрических уравнений, которые в совокупности образуют систему.
В состав системы эконометрических уравнений входят множество зависимых или эндогенных переменных и множество предопределённых переменных (лаговые и текущие независимые переменные, а также лаговые эндогенные переменные).
Системы эконометрических уравнений используются для объяснения текущих значений эндогенных переменных в зависимости от значений предопределённых переменных.
Системы эконометрических уравнений, которые используются в эконометрическом моделировании, подразделяются на три типа.
1. Система независимых эконометрических уравнений вида:
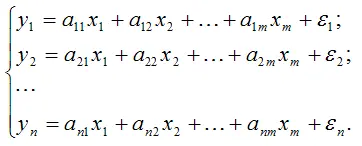
Данная система характеризуется тем, что каждая эндогенная переменная y является функцией от одних и тех же переменных x;
2. Система рекурсивных эконометрических уравнений вида:
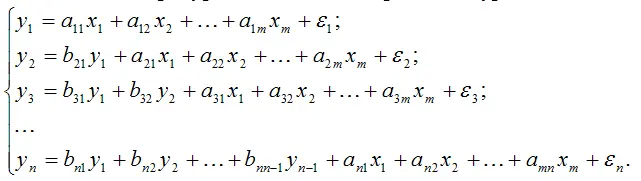
Данная система характеризуется тем, что в каждом последующем уравнении эндогенная переменная выступает в качестве экзогенной переменной;
3. Система взаимозависимых эконометрических уравнений вида:
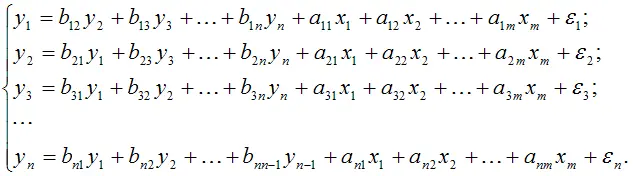
Данная система характеризуется тем, что эндогенные переменные в одних уравнениях входят в левую часть (т. е. являются результативными переменными), а в других уравнениях – в правую часть (т. е. являются факторными переменными).
В системе взаимозависимых уравнений значения результативных и факторных переменных формируются одновременно под влиянием внешних факторов. Поэтому данная система также называется системой одновременных или совместных уравнений.
В системах независимых и рекурсивных уравнений каждое уравнение может рассматриваться самостоятельно, поэтому оценки неизвестных коэффициентов этих уравнений можно рассчитать с помощью классического метода наименьших квадратов.
В системе одновременных уравнений каждое уравнение не может рассматриваться как самостоятельная часть системы, поэтому оценки неизвестных коэффициентов данных уравнений нельзя определить с помощью классического метода наименьших квадратов, т. к. нарушаются три основных условия применения этого метода:
Читать дальшеИнтервал:
Закладка:










