Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

а) модель авторегрессии;

б) модель с распределённым лагом.

Моделью авторегрессииназывается динамическая эконометрическая модель, в которой в качестве факторных переменных содержатся лаговые значения результативной переменной.

Пример модели авторегрессии:

yt=β0+β1xt+δ1yt–1+εt.

Моделью с распределённым лагомназывается динамическая эконометрическая модель, в которую включены не только текущие, но и лаговые значения факторных переменных.

Пример модели с распределённым лагом:

yt=β0+β1xt+β2xt–1+…+βLxt–L+εt.

где L – это величина временного лага (запаздывания) между рядами;

3) динамические модели, в которые входят переменные, отражающие предполагаемый или желаемый уровень результативной переменной или одной из факторных переменных в определённый момент времени ( t+1 ). Величина желаемого уровня является неизвестной и рассчитывается на основании той информации, которая имеется в наличии на предшествующий момент времени ( t ). В зависимости от способа расчёта желаемых переменных различают следующие виды моделей:

а) модель адаптивных ожиданий (МАО);

б) модель частичной (неполной) корректировки (МЧК)

Моделью адаптивных ожиданийназывается динамическая эконометрическая модель, которая учитывает предполагаемое или желаемое значение факторной переменной

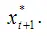
Общий вид модели адаптивных ожиданий:

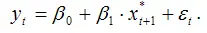
Примером модели адаптивных ожиданий является модель зависимости предполагаемой в будущем периоде ( t+1 ) индексации заработных плат и пенсий на текущие цены.

Моделью частичной (неполной) корректировкиназывается динамическая эконометрическая модель, которая учитывает предполагаемое (или желаемое) значение результативной переменной

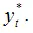
Общий вид модели частичной корректировки:

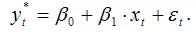
Примером модели частичной корректировки является модель Литнера, которая отражает зависимость желаемого объёма дивидендов

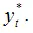
от фактического текущего объёма прибыли xt .

Неизвестные коэффициенты динамических эконометрических моделей нельзя рассчитать с помощью традиционного метода наименьших квадратов, потому что они не будут удовлетворять свойствам несмещённости, состоятельности и эффективности.

Неизвестные коэффициенты моделей авторегрессии оцениваются с помощью метода инструментальных переменных.

Для моделей с распределённым лагом в зависимости от структуры лага для оценивания неизвестных коэффициентов применяются метод Алмон и метод Койка. Суть данных методов состоит преобразовании исходной модели с распределённым лагом к модели авторегрессии, оценки неизвестных параметров которой можно рассчитать с помощью метода инструментальных переменных.

Для определения оценок неизвестных коэффициентов модели адаптивных ожиданий и модели частичной корректировки их также преобразуют в модели авторегрессии.

Моделью авторегрессииназывается динамическая эконометрическая модель, в которой в качестве факторных переменных содержатся лаговые значения результативной переменной.

Пример модели авторегрессии:

yt=β0+β1xt+δ1yt–1+εt,

где β1 – это коэффициент, который характеризует краткосрочное изменение переменной у под влиянием изменения переменной х на единицу своего измерения;

δ1 – это коэффициент, который характеризует изменение переменной у в текущий момент времени t под влиянием своего изменения в предыдущий момент времени ( t–1 ).

Промежуточным мультипликаторомназывается произведение коэффициентов модели авторегрессии ( β1 * δ1) .

Промежуточный мультипликатор отражает общее абсолютное изменение результативной переменной у в момент времени ( t+1 ).

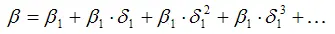
Определение. Долгосрочным мультипликатором называется показатель, рассчитываемый как

Долгосрочный мультипликатор отражает общее абсолютное изменение результативной переменной у в долгосрочном периоде.

Если для модели авторегрессии выполняется условие | δ|<1 , то при наличии бесконечного лага будет справедливым равенство:

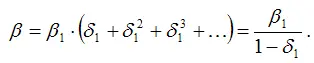
В нормальной линейной модели регрессии все факторные переменные не зависят от случайной ошибки модели. Данное условие для моделей авторегрессии нарушается, потому что переменная yt-1 частично зависит от случайной ошибки модели εt . Следовательно, при оценке неизвестных коэффициентов традиционным методом наименьших квадратов ы получим смещённую оценку коэффициента при переменной yt –1 .

При определении оценок неизвестных коэффициентов модели авторегрессии используется метод инструментальных переменных (IV – Instrumental variables).

Суть метода инструментальных переменных заключается в том, что переменная yt –1 , для которой нарушается предпосылка применения метода наименьших квадратов, заменяется на новую переменную z, удовлетворяющую двум требованиям:

1) данная переменная должна тесно коррелировать с переменной yt–1 : cov(yt–1,z)≠0 ;

2) данная переменная не должна коррелировать со случайной ошибкой модели εt : cov(z,ε)=0 .

Предположим, что на основании собранных данных была построена модель авторегрессии вида:

yt=β0+β1xt+δ1yt–1+εt.

Рассчитаем оценки неизвестных коэффициентов данной модели с помощью метода инструментальных переменных.

В данной модели авторегрессии переменная yt коррелирует с переменной xt , следовательно, переменная yt –1 зависит от переменной xt –1 . Охарактеризуем данную корреляционную зависимость с помощью парной модели регрессии вида:

yt–1=k0+k1xt–1+ut ,

где k0 ,k1 – неизвестные коэффициенты модели регрессии;

ut – случайная ошибка модели регрессии.

Обозначим выражение k0+k1xt–1 через переменную zt –1 . Тогда модель регрессии для переменной yt –1 примет вид: