Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

Примером модели адаптивных ожиданий является модель зависимости размера предполагаемой в будущем периоде ( t+1 ) индексации заработных плат и пенсий на текущие цены, или модель зависимости объёма текущих инвестиций в момент времени t от ожидаемого курса валюты в момент времени ( t+1 ).

Механизм формирования ожиданий в модели адаптивных ожиданий можно представить следующим образом:

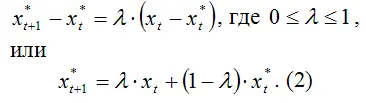
Следовательно, ожидаемое значение переменной xt в следующий момент времени ( t+1 ) можно определить как среднее арифметическое взвешенное значение её фактического xt и ожидаемого

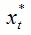
значений в текущем периоде t.

Величина λ называется параметром адаптации. Чем больше величина параметра адаптации, тем быстрее ожидаемое значение адаптируется предыдущим фактическим событиям xt . Чем меньше величина данного параметра, тем ближе ожидаемое в будущем значение

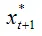
к ожидаемому значению предшествующего периода

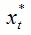
что характеризует сохранение тенденций в ожиданиях.

Модель адаптивных ожиданий содержит предполагаемые значения факторной переменной, которые нельзя получить эмпирическим путём, поэтому применение традиционного метода наименьших квадратов для оценки неизвестных коэффициентов данной модели невозможно.

Для определения оценок неизвестных коэффициентов исходной модели адаптивных ожиданий (1) её необходимо преобразовать.

Подставим выражение (2) в исходную модель (1):

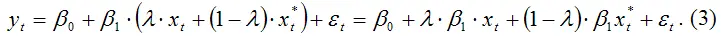
Исходя из предположения о том, что если модель адаптивных ожиданий (1) верна для момента времени t, то она будет верна и для момента времени ( t-1 ), запишем модель адаптивных ожиданий для периода ( t-1 ):

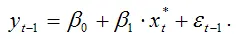
Умножив данное выражение на (1-λ), получим:

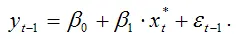
Далее вычтем почленно полученное выражение из модели (3):

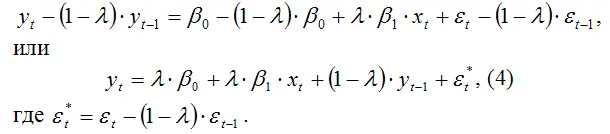
Преобразованная модель (4) является обычной моделью авторегрессии. Оценки неизвестных коэффициентов данной модели можно рассчитать с помощью метода инструментальных переменных. После определения модели авторегрессии можно перейти к оценке параметров исходной модели адаптивных ожиданий (1).

Долгосрочной функцией модели адаптивных ожиданийназывается модель (1), которая характеризует зависимость результативной переменной от предполагаемых значений факторной переменной.

Определение. Краткосрочной функцией модели адаптивных ожиданий называется модель вида [4], полученная в результате преобразований, которая характеризует зависимость результативной переменной от фактических значений факторной переменной.

Моделью частичной (неполной) корректировкиназывается динамическая эконометрическая модель, которая учитывает предполагаемое или желаемое значение результативной переменной

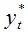
Общий вид модели частичной корректировки:

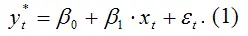
Предполагаемое значение переменной

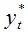
в момент времени t рассчитывается на основании значений фактических (реальных) переменных в предшествующий момент времени ( t-1 ).

Примером модели частичной корректировки является модель Литнера, которая характеризует зависимость желаемого объёма дивидендов

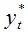
от фактического текущего объёма прибыли xt .

В основе модели частичной корректировки лежит предположение о том, что величина фактического приращения результативной переменной в текущем периоде по сравнению с предшествующим периодом ( yt–yt–1 ) пропорциональна разности между её ожидаемым уровнем и фактическим значением в предшествующий момент времени

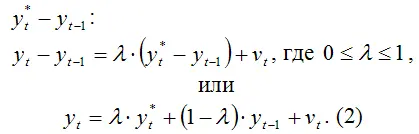
Следовательно, фактическое значение результативной переменной в момент времени t ( yt ) определяется как среднее арифметическое взвешенное значение предполагаемого уровня результативной переменной в тот же самый момент времени

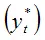
и фактического значений этой переменной в предшествующий момент времени t–1 ( yt –1 ).

Величина λ называется параметром корректировки.

Чем больше значение параметра корректировки, тем быстрее осуществляется процесс корректировки результативной переменной yt .

Если параметр корректировки равен единице, то фактическое значение результативной переменной равно её ожидаемому значению

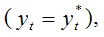
и процесс полной корректировки происходит за один период.

Если параметр корректировки равен нулю, то корректировка результативной переменной yt не происходит вовсе.

Модель частичной корректировки содержит предполагаемые значения результативной переменной, которые нельзя получить эмпирическим путём, поэтому оценивание неизвестных коэффициентов модели с помощью традиционного метода наименьших квадратов невозможно.

Для определения оценок неизвестных коэффициентов исходной модели частичной корректировки (1) её необходимо преобразовать.

Подставим исходную модель (1) в выражение (2):

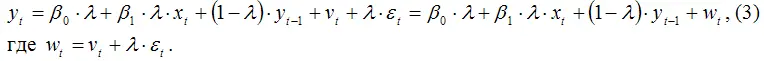
Оценки неизвестных параметров β0 , β1 и λ преобразованной модели можно рассчитать с помощью традиционного метода наименьших квадратов.

Преобразованная модель (3) включает стохастическую объясняющую переменную yt –1 . Но данная переменная не коррелирует с текущим значением совокупной случайной ошибки модели wt, потому что ошибки εt и νt определяются только после расчёта значения результативной переменной yt –1 . Поэтому оценки неизвестных коэффициентов, полученные с помощью традиционного метода наименьших квадратов, будут асимптотически несмещёнными и эффективными оценками.