Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

yt–1= zt–1+ut .

Новая переменная zt –1 удовлетворяет свойствам, предъявляемым к инструментальным переменным:

1) она тесно коррелирует с переменной yt–1 : cov(zt–1,yt–1)≠0;

2) она коррелирует со случайной ошибкой исходной модели авторегрессии εt : cov(εt, zt–1).

Таким образом, исходная модель авторегрессии может быть представлена следующим образом:

yt=β0+β1xt+δ1(k0+k1xt–1+ut)+εt= β0+β1xt+δ1 zt–1+νt,

где νt= δ1 ut+ εt .

На следующем этапе оценки неизвестных коэффициентов преобразованной модели рассчитываются с помощью традиционного метода наименьших квадратов. Эти оценки будут являться оценками неизвестных коэффициентов исходной модели авторегрессии.

Моделью с распределённым лагомназывается динамическая эконометрическая модель, в которую включены не только текущие, но и лаговые значения факторных переменных.

С помощью модели с распределённым лагом можно охарактеризовать влияние изменения факторной переменной х на дальнейшее изменение результативной переменной у , т. е. изменение х в момент времени t будет оказывать влияние на значение переменной у в течение L следующих моментов времени.

Пример модели с распределённым лагом:

yt=β0+β1xt+β2xt–1+…+βLxt–L+εt.

Краткосрочным мультипликаторомназывается коэффициент β1 модели с распределённым лагом

Краткосрочный мультипликатор характеризует среднее абсолютное изменение переменной yt при изменении переменной xt на единицу своего измерения в конкретный момент времени t при элиминировании влияния лаговых значений переменной х .

Коэффициент β 2 модели с распределённым лагом характеризует среднее абсолютное изменение переменной yt в результате изменения переменной х на единицу своего измерения в момент времени t–1 .

Промежуточным мультипликаторомназывается сумма коэффициентов β1 и β 2 модели с распределённым лагом.

Промежуточный мультипликатор характеризует совокупное влияние факторной переменной х на переменную у в момент времени ( t+1 ). Таким образом, изменение переменной х на единицу в момент времени t вызывает изменение переменной у на β1 единиц в момент времени t и изменение переменной у на β 2 в момент времени ( t+1 ).

Средним лагом называется средний период времени, в течение которого будет происходить изменение результативной переменной у под влиянием изменения факторной переменной х в момент t:

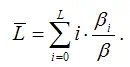
Если величина среднего лага небольшая, то переменная у достаточно быстро реагирует на изменение факторной переменной х .

Если величина среднего лага большая, то факторная переменная х медленно воздействует на результативную переменную у.

Медианным лагомназывается период времени, в течение которого с момента начала изменения факторной переменной х будет реализована половина её общего воздействия на результативную переменную у .

Оценки неизвестных коэффициентов модели с распределённым лагом традиционным методом наименьших квадратов рассчитать нельзя по трём причинами:

1) нарушение первого условия нормальной линейной модели регрессии, т. е. наличие корреляции между текущими и лаговыми значениями факторной переменной;

2) при большой величине лага L уменьшается количество наблюдений, по которым строится модель регрессии и увеличивается число факторных переменных ( xt,xt–1,xt–2,… ), что в конечном результате ведёт к потере числа степеней свободы в модели;

3) наличие проблема автокорреляции остатков.

Данные причины в итоге ведут к нестабильности оценок коэффициентов регрессии, вычисленных с помощью метода наименьших квадратов.

Оценки неизвестных коэффициентов моделей с распределённым лагом рассчитывают с помощью специальных методов, чаще всего с использованием метода Алмон и метода Койка.

Для оценки неизвестных коэффициентов модели с распределённым лагом применяется метод Алмон или лаги Алмон.

Данный метод можно применять к моделям, которые характеризуются полиномиальной структурой лага и конечной величиной лага L :

yt=β0+β1xt+β2xt–1+…+βLxt–L+εt. (1)

Структура лага определяется графическим методом при отражении зависимости параметров при факторных переменных от величины лага.

Алгоритм метода Алмон реализуется в несколько этапов:

Суть метода Алмон состоит в следующем:

1) зависимость коэффициентов при факторных переменных βi от величины лага i аппроксимируется полиномиальной функцией:

а) первого порядка βi=c0+c1*i

б) второго порядка

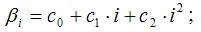
в) третьего порядка

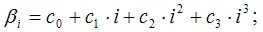
г) в общем случае полиномиальной функцией порядка P:

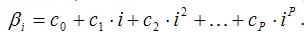
Алмон доказал, рассчитать оценки коэффициентов

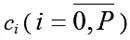
намного проще, чем найти оценки непосредственно коэффициентов βi. Подобный метод оценивания коэффициентов βi называется полиномиальной аппроксимацией.

2) каждый коэффициент модели (1) можно выразить следующим образом:

β1=c0;

β2=c0+c1+…+cP;

β3=c0+2c1+4c2+…+2PcP;

β4=c0+3c1+9c2+…+3PcP;

…

βL=c0+Lc1+L2c2+…+LPcP.

Подставим полученные выражения для коэффициентов β i в модель (1):

yt=β0+c0xt+( c0+c1+…+cP)xt–1+…+( βL=c0+Lc1+L2c2+…+LPcP)xt–L+εt.

3) в полученном выражении перегруппируем слагаемые:

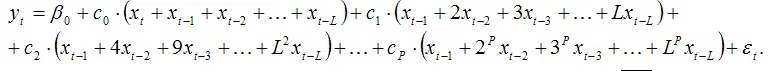
Обозначим слагаемые в скобках при коэффициентах

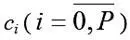
как новые переменные:

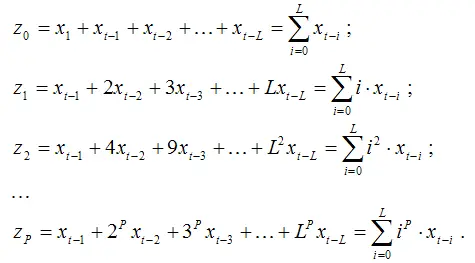
С учётом новых переменных модель примет вид:

yt=β0+c0z0+c1z1+…+cPzP+εt. (2)

4) оценки неизвестных коэффициентов модели (2) можно рассчитать с помощью традиционного метода наименьших квадратов. Далее на основе полученных оценок коэффициентов