Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Это событие-следствие может быть малым приращением пути, пройденного телом, или приростом численности популяции за небольшой промежуток времени. Т. е. пройденный телом путь может быть причиной значения его скорости в данный момент времени (движение частицы в однородном силовом поле) и текущая численность популяции может быть причиной ее текущего естественного прироста, а не наоборот.

Примером функциональной, непричинной (не ПОС и не ООС) связи между переменной и скоростью ее роста может служить связь между средним ежедневным выпуском продукции на некотором предприятии и общим ее количеством, выпущенном с начала года.

Пусть в январе запланировано выпустить некоторое количество продукции, а за каждый последующий месяц в течение года ее выход по сравнению с предыдущим должен быть увеличен на десять процентов. При этом количество ежедневно выпускаемых товаров может быть любым, т. е. никак планом не регламентируется.

Но в конце последнего дня каждого месяца план должен быть выполнен, т. е. должно быть произведено запланированное количество продукции (не больше и не меньше). Связь между усредненным за некоторый небольшой промежуток времени ежедневным и общим количеством продукции, выпущенным с начала года, будет в этом случае функциональной, непричинной. Функциональной в том смысле, что эти средние связаны вполне определенной аналитической зависимостью, а непричинной – в том смысле, что не текущее количество выпущенных товаров причинно определяет прирост и не текущий прирост причинно задает это количество, а делает это управляющая система, реализующая закон, по которому растет как ежедневный прирост продукции (как управляемый случайный процесс), так и общий ее выпуск (как управляемый, эквифинальный, нестационарный случайный процесс), полностью определяемый его суммарной величиной.

Т. е. вероятностный закон, связывающий мгновенное общее количество выпущенной с начала года продукции со скоростью ее производства в каждый момент времени, описывает непричинную, функциональную, а не причинно-следственную связь. Нестационарный управляемый случайный процесс N(t): количество товаров, выпущенных к моменту времени t может считаться эквифинальным в том смысле, что в конце каждого месяца N(t) будет отличаться от планового значения на некоторую относительно небольшую предзаданную величину.

Т. к. количество выпущенных товаров возрастает ежемесячно в одно и то же число раз (в 1,1 раза), то вероятностная, непричинная зависимость между скоростью производства и полным количеством выпущенной с начала года продукции в любой момент времени в течение этого месяца будет примерно линейной. А зависимость количества произведенных товаров от времени в течение года в первом приближении – экспоненциальной.

Если бы такой прирост планировался не на постоянных, а на сокращающихся по закону прогрессии к точке сингулярности отрезках времени, то рост выпущенной продукции был бы гиперболическим. Причем в простейшем случае такого роста функциональная зависимость между скоростью производства и общим выпуском товаров была бы уже не линейной, а параболической. Т. е. описывалась бы законом квадратичного роста (1). (По такому же закону растет и численность населения Земли. И закон квадратичного роста, связывающий эту численность и скорость ее роста, может и не быть причинным законом.)

Здесь мы имеем дело с причинным, вероятностным, целевым (телеологическим) законом или законом с постдетерминацией, связывающим количество выпускаемой ежедневно в течение года продукции (случайную переменную-следствие) с плановым общим ее выходом в конце каждого месяца – причинной целевой переменной, значение которой предопределено в будущем.

При анализе причинного закона с преддетерминацией недостаточно указать формулу, аналитическую зависимость, связывающую каузальные переменные. Необходимо еще описать КАК в пространстве и во времени рост переменной-причины приводит к росту (уменьшению) переменной-следствие.

Данное нами определение причинного закона для двух переменных сформулировано для конкретной задачи исследования законов роста численности популяций и, в частности, закона роста численности населения Земли. Мы не ставили перед собой задачи всесторонне исследовать этот сложный вопрос и давать наиболее общее определение.

Дадим определение закона квадратичного роста как причинного закона, рассматривая (1) как уравнение в конечных разностях (1А), рис. 3.

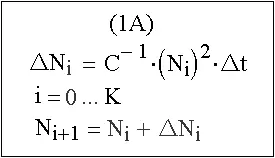
Рис. 3. Решение задачи Коши методом Эйлера.

Пусть в начальный момент времени t 0численность популяции равна N 0. Разобьем промежуток t – t 0на интервалы равной длительности, причем шаг Δt можно сделать «сколь угодно» малым (в разумных пределах).

Введем сеточную функцию дискретного аргумента, вычисляемую в узлах сетки. В момент t 0+ Δt прирост численности найдем по (1А) и определим ее новое значение.

Продолжим итерации, опираясь на (1А) как на рекуррентное соотношение, и вычислим значение численности во всех узловых точках, решив, таким образом, простейшую задачу Коши одношаговым методом Эйлера.

Закон квадратичного роста (1) можно считать причинным законом в том, и только в том случае, если действительный рост численности популяции в точности соответствует этому математическому итеративному алгоритму и удовлетворяет двум следующим условиям:

1.Для описания роста численности может быть введен отрезок времени Δt, с одной стороны, достаточно малый для того, чтобы закон роста мог быть сформулирован в форме дифференциального уравнения, а, с другой стороны, достаточно большой для того, чтобы смогли заработать механизмы этого роста, которые для каждой модели свои. Для изобретательской теории Коротаева Δt – это то время, за которое изобретения «растворятся» в Мир-системе и дадут прирост ΔN. Для феноменологической теории Капицы – это время достаточно большое для того, чтобы накопленная в Ойкумене информация дала неслучайный прирост, пропорциональный квадрату числа связей.

2.Рост численности популяции на любом конечном отрезке времени может быть представлен как причинно-следственная цепь событий(с описанием этих событий в пространстве и во времени от t до t + Δt): …→N→причина роста→прирост ΔN за Δt→N + ΔN→…, привязанных к узлам сеточной функции на оси времени.

В этом, и только в этом случае, закон квадратичного роста (1) может рассматриваться как причинный закон, описывающий автокаталитический, самоускоряющийся процесс, как положительная обратная связь второго порядка. Рост численности любых размножающихся «частиц», происходящий в соответствии с таким причинным законом квадратичного роста, может служить примером режима с обострением.