Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Такие допущения считаются если не очевидными, то вполне правдоподобными и принимаются на веру без доказательства как постулат. Но можно ли в них поверить, ведь постулируется сразу три глобальных причинных закона. Не слишком ли много?

И, кроме того, для их выполнения требуется быстрое распространение изобретений на всю Ойкумену, т. е. единое для всего населения мира информационное поле. Иначе говоря, миф об изобретателях не может существовать без мифа о Мир-системе. На шатком основании выстраивается не менее шаткая надстройка. Т. е. мы имеем здесь дело с мифом в квадрате.

2.Функция распределения множества изобретений по значимости не является равномерной, что противоречит основной предпосылке модели Коротаева об изобретателях и изобретениях. Действительно, изобретательская теория Коротаева предполагает большое количество незначительных изобретений.

На самом же деле главную роль в развитии играют не множественные мелкие изобретения, а немногочисленные крупные открытия, «базисные инновации» (по Л. Нефедову), которые в течение десятилетий после их внедрения играют роль локомотива мировой экономики.

3.Важным допущением модели Коротаева является предположение «больше людей – больше (во столько же раз) изобретателей». Но почему при удвоении численности населения мира число изобретателей также удваивается? – Ведь Мир-система не остается подобной себе до такого удвоения, она изменяется и изменяется при этом качественно: растет продолжительность жизни, общественное благосостояние, процент грамотных людей, меняется возрастной, гендерный состав населения…

Тогда почему процент потенциальных изобретателей, присутствующий в формуле Кремера, остается неизменным? По мере роста уровня благосостояния у все большего числа людей, способных к творчеству, высвобождается свободное время, которое они могут потратить на изобретательскую деятельность.

Следовательно, процент таких людей, потенциальных изобретателей, пропорционален ВВП, приходящемуся на душу населения. Во всяком случае, это кажется вполне правдоподобным. К такому же заключению приводит правдоподобное предположение о том, что процент людей, занимающихся изобретательством, пропорционален не полной численности населения мира, а числу грамотных людей, т. к. неуч − плохой изобретатель.

Но число грамотных людей, так же как и ВВП, приходящийся на душу населения, росли по закону квадратичной C'/(t 0– t) 2, а не простой гиперболы C/(t 0– t), что, кстати, отмечено и самим Коротаевым [20], т. е. эти величины не были просто пропорциональны численности населения мира, а были (в первом приближении) пропорциональны квадрату этой численности.

В таком случае гипотеза Кремера приводит к противоречию: скорость роста численности населения мира пропорциональна кубу этой численности. Иначе говоря, предположение Коротаева о том, что число изобретателей пропорционально численности населения Земли выглядит как подгонка к закону квадратичного роста.

4.Мальтузианское допущение Кремера о том, что рост численности человечества для каждого момента времени в прошлом был ограничен потолком несущей способности Земли, обусловленным уровнем жизнеобеспечивающих технологий, представляется совершенно неприемлемым. С.П. Капица убедительно показал, что рост численности населения мира никогда не зависел ни от каких ресурсов. [1]

5.Уравнение Кремера, на котором построена вся теория Коротаева, выведено в предположении, что численность населения мира каждый раз «мгновенно» вырастает до потолка несущей способности Земли, задаваемого поднявшимся уровнем технологического развития.

На самом же деле, и мы это в дальнейшем обоснуем [76], временем этого переходного процесса, которое мы назвали временем проявления системности, пренебречь нельзя в принципе и уравнение Кремера должно быть уравнением с запаздывающим аргументом. Если бы время запаздывания было значительно меньше характерного времени исторических изменений, равного примерно сорока годам, эффект был бы незначителен и им можно было бы пренебречь.

На самом же деле на всем пути исторического развития эти времена всегда были как минимум соизмеримы или даже бывали такие периоды, когда время запаздывания значительно превосходило характерное время системы. Динамика роста численности, как показывают исследования таких уравнений с запаздыванием, способна принимать колебательный характер. В такой системе, имеющей петлю обратной связи со столь значительной задержкой, возможны даже резонансы: колебания с нарастающей амплитудой. [24]

Чего ни в малейшей степени не наблюдается: «человеческая популяция» во все времена демонстрировала монотонный, устойчивый гиперболический рост с последующим переходом к стабилизации. Все это говорит о неадекватности изобретательской теории Коротаева.

6.Изобретательская теория Коротаева описывает некий усредненный, «среднестатистический этнос», но почему вообще возможно такое усреднение? Способность к размножению и росту численности у разных народов в разные времена могла отличаться в разы.

Так, до начала демографического перехода коэффициент рождаемости в европейских странах не превосходил 3–4. В наше время, после прохождения ими перехода, он составляет 1.4–1.8, что меньше минимально необходимого 2.11 для простого воспроизводства; при этом происходит вытеснение коренного населения выходцами из стран с исламской культурой, где переход еще не начался и этот коэффициент равен восьми.

7.Точность, которую Форстер и его коллеги получили для величин n и t 0, обрабатывая большое количество данных за последние две тысячи лет, вступает в противоречие с изобретательской теорией Коротаева.

Можно ли поверить с учетом всего сказанного, что справедливый лишь в тенденции закон квадратичного роста (1), полученный в предположении инновационной природы роста численности, обеспечивает такую фантастическую точность для показателя степенной функции и точки сингулярности гиперболы Форстера?

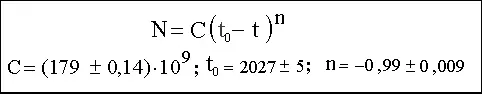
Рис. 2. Результаты обработки Форстером демографических данных за две тысячи лет. Точность показателя степенной функции 1 %, точность в определении точки сингулярности 5 лет.

Показатель степенной функции (n = -0.99 ± 0.01) определяет тип степенного закона. Он равен минус единице с точностью до 1 %, т. е. найденная зависимость является самой простой из семейства гиперболических кривых. Именно ее изучают в курсе средней школы. Все это не может быть делом случая. Несомненно, здесь проявилась важная фундаментальная причина, а вовсе не какая-то тенденция, как считает Коротаев.