Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Но проблема даже не в том, как установилось подобное сочетание параметров (что совершенно непонятно и удивительно), а в том как оно поддерживается в течение сотен миллионов лет. Ведь кислород постоянно воспроизводится в земной атмосфере в процессе фотосинтеза и выводится из нее вследствие процессов горения, дыхания и выветривания. При этом каждую тысячу лет атмосферный кислород полностью обновляется. Какой механизм обеспечивает постоянство концентрации кислорода? Маркс замечает в связи с этим, что термическая и химическая стабильность земной атмосферы скорее похожа на чудо, чем на необходимость.

И вот теперь самое главное – во всех этих рассуждениях не принимался во внимание фактор жизни. По мысли Маргулис и Лавлока именно жизнь выполняет роль регулирующего механизма. Она сама регулирует химический состав и температуру нижних слоев атмосферы. Жизнедеятельность биоты, т. е. всех организмов растительного и животного происхождения, с одной стороны, зависит от состояния биосферы, а, с другой стороны, воздействует на все химические и физические процессы в окружающей среде и, в частности, на процентное содержание атмосферных газов, регулирующих температуру Земли. Например, потепление ведет к росту биомассы, для которой необходим углекислый газ. Снижение процентного содержания углекислоты в атмосфере ведет к уменьшению парникового эффекта и к похолоданию. Существует множество таких регулирующих обратных связей, многие из них не изучены, о некоторых мы даже не подозреваем, причем все они изменяются с течением времени» [22].

Согласно концепции Геи Лавлока, гомеостаз биосферы обеспечивался во все времена эквифинальностью процесса ее эволюции. Эквифинальность здесь означает способность динамической регулирующей системы использовать множество существующих и меняющихся связей в биосфере для обеспечения постоянства среднегодовой температуры и других важных управляемых переменных гомеостаза.

Именно благодаря гомеостазу на планете образовалась жизнь, стала возможной ее эволюция в течение миллиардов лет пока, наконец, не появился человек, появился и всего за несколько тысяч лет социального развития создал ноосферу.

Ноосфера – это результат эволюции биосферы, последняя и высшая ступень в ее развитии. После демографического перехода, происходящего благодаря множеству до конца не изученных причин, «выйдет на полку», стабилизируется (предположительно, в рамках гипотезы) ряд важных показателей глобального развития.

Дальнейшая эволюция станет новым витком спирали, когда будет сохраняться уже гомеостаз ноосферы – высшей стадии развития биосферы; сохраняться благодаря множеству возникающих и исчезающих регулирующих связей самой разнообразной природы. Процесс будет длиться тысячи лет до тех пор, пока в недрах эволюционирующего человечества не возникнет новый вид, средой обитания которого будет уже вся Солнечная система.

Провозглашение принципа демографического императива или гипотезы синхронного гиперболического роста показателей глобального развития не освобождает еще от необходимости давать объяснение пакету законов на рис. 1. Должен существовать причинный закон, полностью объясняющий парадоксальную независимость важнейших показателей роста и развития от ресурсов.

Этот закон должен существовать и в том случае, если связи на рис. 1 не являются причинно-следственными. И все эти функциональные зависимости должны вытекать из этого, неизвестного пока закона. Попробуем сформулировать такой феноменологический закон, причем рассматривать его будем только как пример, как альтернативу неработающему причинному закону квадратичного роста.

Любая феноменологическая теория предполагает введения ряда постулатов. Начнем с определения главного цикла роста и развития, длительность которого равна характерному времени исторических изменений τ = 40 лет. Это время впервые было введено С.П. Капицей в рамках его феноменологической теории гиперболического роста населения Земли.

К сожалению, С.П. Капица не попытался связать его ни с каким существующим циклическим историческим процессом, что, по нашему мнению, является существенным недостатком его модели. Будем считать таким циклическим процессом экономический цикл Кондратьева, который в данной феноменологической схеме определим как главный цикл эволюции и истории.

Второй шаг в определении этого феноменологического закона – разбиение всей эпохи роста от начала неолита (8 тыс. лет до н. э.) до сингулярности гиперболы Форстера (2022 год) на 256 циклов. Постулируем относительный прирост населения мира за каждый такой цикл равным члену гармонической последовательности : 1/255, 1/254… 1/3, 1/2, 1.

Допустим, что численность населения Земли на момент начала неолита была равна 16 млн человек. Тогда через 40 лет, т. е. спустя один цикл, эта численность станет равной 16 + 16/255 = 16.06 млн чел., еще через 40 лет: 16.06 + 16.06/254 = 16.12 млн чел. и т. д.

В результате за 255 циклов, к 1982 году, численность за цикл удвоится и станет равной ее значению на момент начала неолита, умноженному на 256, т. е. k*4.3 млрд человек. Причем все 255 ее значений будут лежать на гиперболе Форстера.

Сформулируем причинный закон с постдетерминацией, способный объяснить феномен гиперболического роста, в виде принципа эквифинальности роста численности населения Земли:

Гиперболический рост происходит в течение 255 циклов. Зависимость численности и скорости ее роста от времени внутри каждого такого цикла могут быть произвольными при том обязательном условии, что в момент завершения цикла относительный прирост за цикл должен соответствовать очередному члену гармонической последовательности: от 1/255 – до 1.

Говоря о моменте завершения цикла, будем иметь в виду не точку на оси времени, а некоторый интервал, длительность которого гораздо меньше характерного времени τ.

Устойчивость смоделированного здесь роста есть выражение программы эквифинальности по определению. Примером аномальной устойчивости роста может служить последний «гиперболический» 255-й цикл мировой демографической системы (1942–1982 гг.), в течение которого программа эквифинальности, всего за 20 лет вернула, несмотря на значительные потери в мировых войнах, рост на «плановую » гиперболу , в результате чего численность за этот цикл удвоилась:

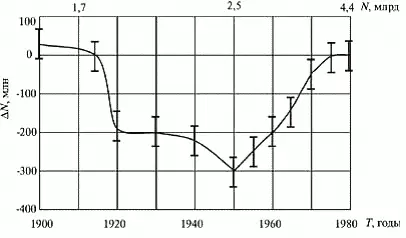
Рис. 1. Возврат роста на «плановую » гиперболу после двух мировых войн за 20 лет, 1955–1975 гг.