Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Остается, правда, непонятным как Холмс различал тонкую грань между неправдоподобным и невозможным. Но на то он и величайший сыщик всех времен и народов.

Закон квадратичного роста как функциональная, непричинная связь вытекает непосредственно из принципа эквифинальности циклического роста численности. Действительно, поскольку гипербола роста полностью предопределена программой эквифинальности как сеточная функция, то средняя скорость роста за цикл может быть вычислена с помощью закона квадратичного роста.

По мнению С.П. Капицы, «…секрет гиперболического, взрывного развития состоит в том, что скорость роста пропорциональна квадрату численности населения мира» [1]. На самом же деле главный секрет здесь в том, что гиперболический рост численности популяций любых организмов, а также множества частиц в физических и химических реакциях под действием общесистемного причинного закона (1) – НИКОГДА не встречается в природе.

В дальнейшем, если это не будет оговорено специально, закон (1) будем считать причинным законом в том смысле, в каком он был определен нами ранее. Таковым же, несомненно , считал этот закон и С.П. Капица, интерпретируя его как закон «коллективного взаимодействия».

Рис. 1. Закон квадратичного роста. Скорость роста численности населения мира пропорциональна квадрату численности.

В своей книге «Парадоксы роста. Законы развития человечества» С.П. Капица приводит графики линейного, экспоненциального и гиперболического роста в качестве иллюстрации возможных сценариев роста населения Земли. [21]

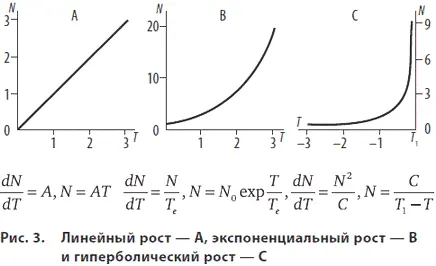
Рис. 2. Возможные сценарии роста численности человечества. Скорость роста постоянна или пропорциональна первой и второй степени численности.

Законы роста как причинные законы здесь схожи, но рост в каждом из трех случаев имеет свои особенности. Так, линейный и гиперболический рост как степенные законы самоподобны, чего не скажешь об экспоненциальном росте. Кроме того, считая закон (1) причинным законом, С.П. Капица акцентирует внимание читателя на том, что численность популяции устремляется к бесконечности за конечный промежуток времени.

Что в случае роста численности человечества приводит, по его мнению, к режиму с обострением, выход из которого С.П. Капица, используя терминологию термодинамики, называет фазовым переходом. В этом и состоит, по мнению С.П. Капицы, главное отличие моделей гиперболического и экспоненциального роста.

После прочтения этого текста и просмотра иллюстраций у читателя возникает впечатление, что закон квадратичного роста как причинный закон явление обычное и встречается в природе достаточно часто. С.П. Капица в своей книге [21] приводит тому ряд примеров. На самом же деле между законами экспоненциального и гиперболического роста численности популяции (законами В и С) лежит непреодолимая пропасть:

Если численность популяции растет по экспоненциальному закону, то для любого момента роста, независимо от его расположения на оси времени, существует такой отрезок времени, неизменный на всей шкале этого роста, в течение которого ее численность удваивается; т. е. рост здесь происходит по закону геометрической прогрессии на последовательности интервалов времени равных по своей длительности. Поэтому закон экспоненциального роста, в отличие от закона степенного роста, имеет встроенный масштаб времени: неизменное, не зависящее от численности популяции, время удвоения ее численности.

Для гиперболического роста, подобного росту населения Земли, также можно подобрать такую последовательность интервалов времени. Отличие здесь в том, что длительность этих интервалов удвоения численности не остается постоянной, как в случае экспоненциального роста. А сокращается по закону той же самой прогрессии,согласно которому растет численность по истечении каждого такого интервала (т. е. удвоение численности достигается на каждом последующем интервале за время в два раза меньшее, чем на предыдущем).

И сходится эта последовательность к некоторой точке на оси времени – точке сингулярности гиперболы роста. Поскольку численность популяции при этом за конечное время неограниченно возрастает, потенциальная бесконечность идеального экспоненциального роста трансформируется здесь в актуальную бесконечность идеального гиперболического роста. Потенциальная возможность неограниченного возрастания численности идеального экспоненциального роста качественным образом отличается от актуальной бесконечности, которой достигает численность в точке сингулярности идеального гиперболичесого роста.

При первом чтении приводимые далее примеры можно пропустить.

Для более ясного представления о том, что такое причинный закон рассмотрим несколько примеров экспоненциального роста:

• Размножение микроорганизмов в чашке Петри с питательной средой;

• Рост числа разделившихся ядер в цепной ядерной реакции;

• Экспоненциальный рост популяции животных с полигамной ориентацией;

• Экспоненциальный рост популяции моногамных животных.

Во всех случаях прирост численности «частиц» пропорционален их общему числу N, но причинно-следственная цепь событий, создающая в каждой системе этот прирост ΔN за малый промежуток времени Δt, в каждом из четырех приведенных примеров будет своя.

Так, каждый из разделившихся микроорганизмов ничем не отличается от материнского и продолжает участвовать в процессе размножения точно в таком же качестве. Чего не скажешь про осколки разделившегося ядра в цепной ядерной реакции, которые никакого участия в дальнейшем размножении распавшихся ядер уже не принимают.

В случае полигамии любая пара противоположного пола может дать потомство, в то время как в популяции моногамных животных пары устойчивы и не имеют других партнеров.

Несмотря на различную природу роста численности таких популяций, сама схема роста во всех случаях одинакова: … → N → события определяющие прирост → прирост ΔN за Δt → N + ΔN →… Здесь прирост ΔN за малый промежуток времени Δt складывается с текущей численностью N, образуя при этом элементарное звено причинно-следственной цепи.

События, включенные в это звено, в каждом случае свои, но объединяет их одинаковый, экспоненциальный механизм роста. Закон экспоненциального роста для всех приведенных примеров может считаться причинным законом , т. к. существуют эндогенные события-причины, т. е. события, вызванные внутренними системными факторами, приводящими к приросту ΔN.