История и антиистория. Критика «новой хронологии» академика А.Т. Фоменко

где n — число членов рядов X i и Y i , а число t определяется вероятностью, с которой мы хотим быть уверены в значимости корреляции (например, для 50% уверенности в существовании связи t = 0.6, для 99% — t = 3).

Коэффициент регрессии по своему смыслу — это угловой коэффициент прямой, которая наиболее близко проходит через точки с координатами ( X i , Y i ). Когда все n точек не лежат на одной прямой, ее проводят так, чтобы сумма квадратов расстояний от этих точек до прямой была минимальной. Формула для коэффициента регрессии более сложна, чем для линейной корреляции, поэтому мы ее не приводим, подчеркнем только, что и здесь важна мера ошибки коэффициента регрессии, т.е. насколько хорошо указанные точки «ложатся» на прямую линию. Значения коэффициентов регрессии и линейной корреляции хорошо согласуются между собой — если коэффициент корреляции показывает наличие линейной связи переменных, то и ошибка коэффициента регрессии мала и наоборот.

Почему же автор не использует эти или иные статистические коэффициенты для оценки связи (1)? Мы не найдем в его книге ответа на этот вопрос. Вместо известных коэффициентов А. Т. Фоменко вводит свою собственную меру близости для рядов максимумов Л ( X , Y ). С его точки зрения, эта мера носит вероятностный характер, т.е. определяет «вероятность случайного совпадения лет» в сравниваемых рядах (мы чуть ниже проанализируем это утверждение). Впрочем, чем бы она ни была, если эта мера вводится корректно, то ее результаты должны согласовываться с приведенными выше коэффициентами.

Чтобы это проверить, опишем, как вычисляется Л ( X , Y ). Идея получения этого коэффициента состоит в сравнении некоторых объемов в n- мерном пространстве, где размерность пространства n совпадает с наибольшей из длин рядов X i и Y i . Данным рядам сопоставляются соответственно две точки n -мерного пространства X ( X 1 , X 2 , … , X n ) и Y ( Y 1 , Y 2 , … , Y n ). Между этими точками (как и в обычном двух и трехмерном пространстве) определяется декартово расстояние

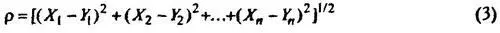
Сразу же обращает на себя внимание вопрос — как быть в случае, если число максимумов в анализируемых хрониках различно? Корректная статистическая процедура требовала бы, чтобы сравнивались ряды с наименьшей из двух длин, т.е. из большего ряда выбирались бы последовательности чисел с длиной равной длине меньшего ряда, затем для каждой пары вычислялся бы коэффициент корреляции и делались бы соответствующие выводы о возможности линейной связи. Однако, автор идет по совершенно иному пути (ничем это не мотивируя) — выбирает наибольшую длину и предлагает считать в меньшем из рядов некоторые максимумы кратными , т.е. слившимися в одну точку, а соответствующие недостающие координаты X i — равными 0. Ясно, что никакого исторического смысла такой кратный максимум не имеет, что же касается математической стороны, то очевидна неоднозначность процедуры выбора кратных максимумов, которая существенно влияет на подсчет Л ( X , Y ), о чем мы еще скажем ниже.

Таким образом, координаты точек X и Y являются целыми положительными числами или нулями, и при этом удовлетворяют условию

где А — полная длина хронологического отрезка, который описывают хроники. Напомним, что по условию, обе хроники описывают одинаковые по продолжительности промежутки времени. Поскольку числа Xi являются расстояниями между соседними максимумами хроники, их полная сумма и должна равняться полной временной протяженности хроники, т.е. А . То же справедливо и для второй хроники Y i .

Множество точек с целочисленными неотрицательными координатами, удовлетворяющими условию (4), автор обозначает Ш и придает ему смысл полного набора всех возможных хроник, которые описывают хронологический промежуток длины A . Каждой точке множества Ш соответствует некоторый набор максимумов, а ему, в свою очередь, некоторая «виртуальная» хроника, что и позволяет автору придать вводимому ниже коэффициенту вероятностную интерпретацию.

Коэффициент Л ( X , Y ) равен отношению количества точек из множества Ш , которые лежат к точке X ближе чем точка Y (в смысле декартового расстояния (3)), к полному числу точек множества Ш . Последнее число, как только что говорилось, по мысли автора — это полное число возможных хроник на данном отрезке длиной A . Величина Л ( X , Y ) называется «вероятностью случайного совпадения лет» (ВССЛ). Таким образом, если, например, Л ( X , Y ) = 10 −6, то это должно означать, что из миллиона наугад взятых хроник, описывающих промежуток времени данной длины, только одна находится к хронике X также «близко», как и хроника Y . Отсюда легко сделать вывод — раз чрезвычайно мала вероятность того, что столь близкое совпадение хроник X и Y случайно, то они обязаны описывать одни и те же события, что и требуется доказать автору.

Неправда ли, все это звучит весьма убедительно? И, конечно, нельзя упрекнуть читателей, которые, не проникая глубже в методику Фоменко, остаются здесь вполне убежденными в достоверности оценок, получаемых с помощью Л ( X , Y ). И, однако, это не так.

Начнем, сперва, с возражений чисто теоретического характера. Замечательным свойством меры Л ( X , Y ) является ее некоммутативность, поскольку в общем случае

Л ( X , Y ) ≠ Л ( Y , X )

Чтобы в этом убедиться, достаточно простейшего примера: А =2, n =2, X (2, 0), Y (1, 1), тогда Л ( X , Y )=2/3, а Л ( X , Y )=1. Некоммутативность ставит под сомнение саму возможность сделать из этого коэффициента какой-нибудь вывод, ведь если хроника X близка к Y по мере Л ( X , Y ), то вовсе необязательно, что Y также близка к X по мере Л ( X , Y ). Очевидно, что автору необходимо как минимум каждый раз, сравнивая хроники, определять обе меры и предъявлять их читателю, а если они совпадают, специально оговаривать этот случай. К сожалению, мы не найдем этого в цитируемой книге. Только в 3-ем ее издании (1999 г.) мы видим, что автор заменяет Л ( X , Y ) на среднее значение Л ( X , Y ) и Л ( Y , X ), с помощью этого добиваясь коммутации. Однако, замечательно, что при этом автором не исправлено ни одно из посчитанных еще в 1-м издании книги конкретных значений коэффициента, что вызывает у читателя законные вопросы.