История и антиистория. Критика «новой хронологии» академика А.Т. Фоменко

Вторым важным замечанием является отсутствие связи между выводами, получаемыми с помощью Л ( X , Y ), и выводами, которые дают стандартные коэффициенты линейной корреляции и регрессии. Убедимся в этом на конкретном примере. Здесь и далее в примерах мы будем полагать значения А =450 лет, и n =15 — эти числа, с одной стороны, удобны для вычислений, а с другой, почти не отличаются от параметров ключевой «совпадающей» пары «Новой хронологии»: Тит Ливий — Грегоровиус (см. ниже). Рассмотрим следующие два ряда по 15 чисел с суммой 450 (они были получены, да поверит нам читатель, не подбором, а наугад, с использованием датчика случайных чисел [250] Все вычисления нашей статьи проводятся с помощью стандартных функций программы Microsoft Excel 97. )

X (25, 24, 24, 22, 28, 23, 32, 33, 37, 25, 32, 39, 32, 33, 41)

Y (36, 28, 23, 38, 20, 35, 31, 26, 28, 31, 30, 27, 39, 22, 36)

Даже при тщательном взгляде на ряды, увидеть в них какую-либо корреляцию, напоминающую связь (1), сложно. Об этом же свидетельствует и коэффициент линейной корреляции, дающий малое значение, равное

r = −0.101

При этом, чтобы сделать вывод о существовании связи хотя бы с 50% вероятностью (см. (2')), требовалось бы значение r по модулю превосходящее 0.6/ √ 15 = 0.185, достоверная же оценка существования корреляции (на уровне 99%), требует значений коэффициента | r | > 3 / √ 15 = 0.77.

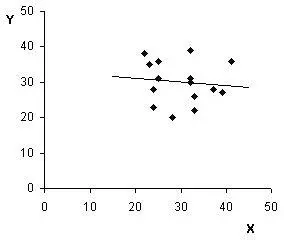
Вычисление регрессионной связи рядов X и Y иллюстрирует следующий рисунок. На нем отсутствует какое-либо выделенное направление в распределении точек, соответствовавшее бы их линейной связи, что и доказывают следующие статистические показатели. Прямая, подобранная по методу наименьших квадратов (см. рис.), обладает коэффициентом регрессии

k = −0,098.

(в случае связи (1)этот коэффициент с необходимостью равнялся бы единице). При этом средняя ошибка коэффициента регрессии μ = 0.268, т.е. более чем в два раза превосходит абсолютное значение самого коэффициента, что не позволяет говорить о какой-либо значимости линейной связи.

Итак, и коэффициент линейной корреляции, и коэффициент регрессии отвергают возможность существования связи (1)для данных рядов X и Y . Тем не менее удивительным будет узнать, что коэффициент Л ( X , Y ) определяет эти ряды как зависимые друг от друга, с вероятностью случайного совпадения не более 2 шансов на миллион ( Л ( X , Y ) <2x10 −6).

Расскажем подробнее, как получается эта оценка. Для n , много больших единицы при вычислении Л ( X , Y ) автор заменяет подсчет целочисленных точек вычислением объемов соответствующих множеств, т.е.

Здесь V n−1( Ш' ) — ( n −1)-мерный объем множества Ш' , которое состоит уже не только из целочисленных, но из всех n -мерных точек с неотрицательными координатами, удовлетворяющих условию (4), а V n−1( X , ρ) — ( n −1)-мерный объем той части Ш' , точки которой лежат ближе к точке X , чем расстояние r до точки Y , вычисленное согласно (3). Из элементарных геометрических формул легко найти, что,

Величина же V n−1( X , ρ) равна объему некоторой части ( n −1)-мерного шара с центром в точке X и радиусом ρ (весь этот шар лежит в ( n −1)-мерной гиперплоскости, заданной условием (4), но может содержать точки с отрицательными координатами, поэтому в множество Ш' входит только часть шара). Ясно, что V n−1( X , ρ) не может превосходить полного объема ( n −1)-мерного шара радиуса ρ, который легко вычисляется, и таким образом имеем (для нечетных n , как в нашем примере) [251] Ср. Фоменко А. Т. Некоторые статистические закономерности распределения плотности информации в текстах со шкалой // Семиотика и информатика. М., 1980. Вып. 15. С. 107.

Подставляя эту оценку в формулу (5)мы получим искомую границу сверху на значение Л ( X , Y ).

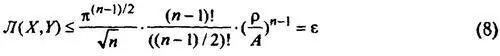
Неравенство (8)переходит в равенство, если шар V n−1( X , ρ) целиком лежит в множестве Ш . Когда это же выполнено и для V n−1( Y , ρ), то мера коммутативна и

Оценка (8)играет большую роль для понимания смысла и значимости коэффициента Л ( X , Y ).

1) Она объясняет происхождение «малых чисел» , которые постоянно встречаются в работах Фоменко, и якобы, гарантируют его результатам абсолютную достоверность. Дело в том, что в (8)отношение ρ/ A , будучи числом меньшим единицы, возводится в большую степень ( n −1) и соответственно, по известному математическому свойству, становится очень малым. Так, в нашем примере, ρ=33.3 года, ρ/ A = 0,074, но после возведения в 14 степень верхняя граница коэффициента Л ( X , Y ) оказывается равной ε = 2x10 −6.

2) Обнаруживается «сверхчувствительность» коэффициента к изменениям положения максимумов. Например, если расстояние — изменится на один год, то пользуясь формулой (8')для коммутативных коэффициентов, можно оценить относительное изменение коэффициента Л ( X , Y )

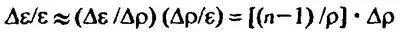
Полагая в нашем примере Δρ = 1 год, ρ = 33 года, получим, что значение коэффициента изменится на 43%, т.е. почти наполовину. Впечатляют оценки и для больших изменений: если расстояние изменить на 50% (уменьшить вполовину), то ε уменьшится в 2 14, т.е. более чем в 16 тысяч раз! Эти изменения совершенно не сопоставимы к обычной чувствительностью статистических коэффициентов (например, чувствительность коэффициента корреляции просто линейно связана с изменениями начальных данных).

Значение Л ( X , Y ) имеет высокую чувствительность и к числу n (т.е. к изменениям числа максимумов и соответствующего количества членов ряда X i или Y i ), Для обычных статистических коэффициентов (см. (2')) значимость обратно пропорциональна √n, и, если n много больше единицы, то при небольшом его изменении оценки значимости коэффициентов корреляции или регрессии практически не изменятся. В то же время, скажем, если в нашем примере мы произвольно выделим еще по 2 новых максимума в каждой из "хроник" X и Y (т.е. изменим n с 15 до 17), то расстояние ρ при этом изменится не слишком значительно, зато уровень коэффициента Л ( X , Y ) упадет в 2 раза. Из (8')для коммутативных коэффициентов следует: