История и антиистория. Критика «новой хронологии» академика А.Т. Фоменко

Мы неоднократно упоминали «вероятность» случайного совпадения максимумов в хрониках, которую автор получает, вычисляя коэффициент Л ( X , Y ). Но очередное возражение, которые мы сейчас сделаем, состоит в том, что такая интерпретация Л ( X , Y ) является крайне неточной, и величина ее ошибки опять-таки сильно зависит от параметров A и n .

В самом деле, если эта интерпретация верна, необходимо, чтобы анализируя случайно выбранную хронику методом локальных максимумов, можно было с равной вероятностью получить любую точку из множества Ш , иначе говоря распределение «виртуальных» хроник (длины А лет) по множеству Ш было бы равномерно. Вот доводы автора: «Равномерность распределения случайного вектора C на множестве Ш может быть обоснована тем, что вектор С изображает точки максимумов функции объема »глав« текстов, описывающих заданный период (A, B), а поскольку наша модель воспроизводит механизм потери и утраты информации, то равновероятна утрата любого документа, описывающего какие-то события из (A, B). При гибели, например, архива, равновероятно уничтожение любого текста». [254] Указ. соч. С. 109.

Из этого рассуждения можно уяснить — автор предполагает, что каждой точке множества Ш соответствует некоторая своя «виртуальная» хроника, и поскольку вероятность сохранения или утраты любой хроники одинакова, то и вероятность встречаемости каждой точки из Ш одинакова. Это было бы верно, но, к сожалению для автора, целые группы точек из множества Ш соответствуют всего одной «виртуальной» хронике.

Это напрямую связано с ничем не мотивированным предположением автора о существовании кратных максимумов и, соответственно, наличием наборов X i с нулевыми координатами. Если «виртуальная» хроника имеет m различных максимумов ( m < n −1), то она допускает (с учетом того, что первое и последнее значения ряда — т.е. соответственно, расстояния от начала (конца) отрезка до первого (последнего) максимума — фиксированы) С m −1 n −2= ( n −2)!/( m −1)! ( n−m −1)! способов расстановки кратных максимумов, и следовательно, ровно столько точек из множества Ш , содержащих на месте кратных максимумов нулевые координаты, и соответствует этой хронике. Утрата этой «виртуальной» хроники (равновероятная среди других) немедленно влечет за собой утрату не одной, а всех С m−1 n−2точек из множества Ш . Поэтому равномерность распределения случайного вектора по множеству Ш нарушается, а точки с нулевыми координатами имеют меньший статистический вес, чем остальные.

Легко оценить общее количество точек, в которых нарушена равномерность распределения. С помощью элементарной комбинаторики можно найти, что полное число точек в множестве Ш равно C n−1 A+n−1, а число точек в Ш , имеющих все координаты ненулевыми, — C n−1 A. Их отношение равно

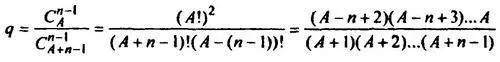
Для наших модельных параметров A=450, n=15 получаем q=65%, а это значит, что для прочих (1−q) = 35% точек множества Ш , имеющих одну или несколько нулевых координат, равномерность распределения не выполняется.

Однако, и оставшиеся ненулевые точки отнюдь не все встречаются с равной вероятностью. Дело в том, что, поскольку автор требует существования локального максимума лишь в одной точке, то в числовых последовательностях не может встречаться расположение максимумов в двух идущих подряд датах, промежуток между которыми — 1 год. Это значит, что точки множества Ш , у которых одна из координат (кроме первой и последней) равна 1, вообще не соответствуют никакой «виртуальной» хронике.

Наконец, не можем не отметить, еще одну особенность применения кратных максимумов. Автор пишет, что перебрав все варианты их расстановки и вычислив для каждого соответствующие коэффициенты, «в качестве Л ( X , Y ) возьмем наименьшее из всех получившихся таким образом чисел». [255] Указ. соч. С. 108. Однако, почему наименьшее , когда статистическая корректность требует из всех оценок выбирать наиболее осторожную, которая соответствует наибольшему из коэффициентов, или, в крайнем случае, усреднять оценки, но уж никак не брать из них наилучшую.

Проведенный анализ, на наш взгляд, убедительно доказывает статистическую некорректность применения методики локальных максимумов для анализа «совпадения» хроник и получения соответствующих «хронологических сдвигов». Разобранные выше основные возражения — несоответствие результатов методики стандартным статистическим коэффициентам, сверхчувствительность и внутренняя природа появления «малых чисел», некорректность вероятностной интерпретации, а также множество более мелких замечаний отвергают возможность использования Л ( X , Y ) для получения значимых статистических результатов (по крайней мере, без дополнительного и тщательного анализа). Тем не менее, мы не ограничимся этими возражениями, и последнюю часть работы посвятим разбору сопоставления по методике Фоменко хроник Тита Ливия и Ф. Грегоровиуса, чтобы на конкретном материале доказать недостоверность полученного им «базового хронологического сдвига».

Активно используемый в книгах по «Новой хронологии» результат состоит в следующем: хроника средневековой истории Рима, изложенная Ф. Грегоровиусом (начиная с 300 г. н.э.), совпадает с хроникой Тита Ливия с ВССЛ 6x10 −10(на отрезке с 1 до 461 г. от основания Рима, т.е. с 753 по 293 г. до н.э.), а также совпадает с объединением книги Тита Ливия и «Очерков по истории древнего Рима» В. С. Сергеева (еще на более широком отрезке с 1 до 519 г. от основания Рима) с ВССЛ 6x10 −11. Тем самым с почти «абсолютной» достоверностью события средневековой и античной истории Рима совпадают, являясь историческими «дубликатами» со сдвигом в 1053 г. Проверим этот результат.

Уже при первом взгляде на анализируемые автором тексты, видны их особенности, не укладывающиеся в стандартную схему методики.

Сочинение Тита Ливия, действительно, можно считать примером погодного изложения событий, но с определенного момента, а именно, с 245 г. — первого года римской республики, когда был установлен ее государственный строй, и в частности, ежегодная смена консулов. Именно с избрания консулов на следующий год и начинает любую свою «погодную» запись Ливий. По этому избранию можно всегда определить начало следующего года и сопоставить каждой записи соответствующий год от основания Рима.