История и антиистория. Критика «новой хронологии» академика А.Т. Фоменко

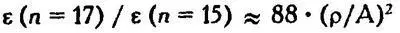
Таким образом, падение будет тем больше, чем меньше «расстояние» между X и Y , так, например, для ρ = 15 лет при том же изменении n уровень коэффициента Л ( X , Y ) упадет уже в 10 раз. Следовательно, при сопоставлении разных пар хроник с разным числом локальных максимумов значения коэффициентов Л ( X , Y ) несопоставимы друг с другом, поскольку каждый раз уровень значимости коэффициента должен определяться отдельно, в зависимости от числа n . В указанной книге А. Т. Фоменко такой анализ отсутствует.

Итак, чувствительность коэффициента Л ( X , Y ) служит существенной проблемой и обостряет проблему интерпретации результата, в то же время обычные статистические коэффициенты полностью лишены этого недостатка.

3) Разберем теперь некоторые конкретные значения коэффициента. Предположим, что в двух хрониках соответствующие промежутки между максимумами отличаются не более чем на Δ лет, т.е. для любого номера i

Если считать, что хроники описывают одинаковые события, то величина Δ имеет смысл наибольшей ошибки хрониста при определении промежутка между последовательными событиями (максимумами). Подставляя неравенства (9)в расстояние (3), получаем, что ρ ≤ √n, что в свою очередь позволяет подставить это расстояние в неравенство (8). Окончательно, мы получаем зависимость ε(Δ), график которой в логарифмическом масштабе изображен на рисунке (здесь по-прежнему, A =450, n =15; по вертикальной оси отложен десятичный логарифм от ε).

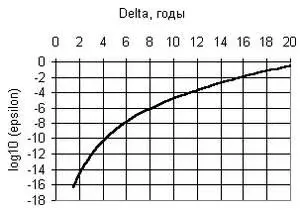
Из графика видно, что Л ( X , Y ) не превосходит 1% при Δ = 16 лет. Иными словами, все хроники на данном отрезке, в которых максимумы различаются не более, чем на 16 лет, можно считать совпадающими, с вероятностью случайного совпадения 1 шанс из 100. Не будем обсуждать с исторической точки зрения, могут ли хроники, описывающие одинаковые события, различаться во датировках на 16 лет (ответ, конечно, зависит от древности хроник), но обратим внимание, что эта ошибка превосходит половину среднего временного промежутка между последовательными событиями X ср= Y ср= A/n = 30 лет. Итак, располагая события по хронологической оси, создатель хроники может допускать ошибки более 50% в определении каждого промежутка, и тем не менее хроники будут трактованы как совпадающие с вероятностью в 99%. Очевидно, что коэффициент Л ( X , Y ), с одной стороны, для действительно зависимых хроник, позволяет хронисту делать огромные ошибки, с другой стороны в пределы этих ошибок могут попасть и совершенно независимые хроники, которые придется интерпретировать как совпадающие с вероятностью 99%.

К чести автора, надо заметить, что вероятность 99% он еще не считает абсолютной для определения тождественности хроник, а существенно опускает границы значимости своего коэффициента. Это делается им на основании «вычислительного эксперимента». В частности, он замечает, что «для независимых текстов число Л ( X , Y ) колеблется от 1 до ? при количестве локальных максимумов от 10 до 15» (заметим, что в последнем случае, когда независимые тексты имеют ВССЛ равной 1/100, как раз и должно реализоваться одно «случайное совпадение» из 100!). Эти значения «разительно отличаются от типичных значений 10 −12– 10 −6для заведомо зависимых текстов (с аналогичным количеством максимумов)». [252] Фоменко А. Т. Методы статистического анализа нарративных текстов и приложения к хронологии. М., 1990. С. 110. Из слов автора следует, что рассмотренный нами выше пример с Л ( X , Y ) <2x10 −6(выбранный, как говорилось, наугад), на самом деле соответствует заведомо зависимым текстам! При этом, и в нашем примере максимальная ошибка D = 16 лет (хотя и достигается не по всем координатам) превосходит половину среднего расстояния между максимумами.

Приведенный нами пример, в котором пара хроник с отсутствующей по стандартным статистическим критериям корреляцией, тем не менее, соответствует зависимым текстам, не только говорит о завышенных автором уровнях значимости, но и вообще ставит под сомнение корректность оценок его «вычислительного эксперимента». Правда, чуть ниже автор еще раз оговаривается, что зависимыми можно считать тексты с коэффициентом меньше 10 −8. На нашем графике этому значению Л ( X , Y ) соответствует Δ = 6 лет, т.е. определяя промежутки между узловыми событиями, наш хронист может ошибаться всего лишь на 20% от среднего расстояния между ними. И эта оценка также представляется нам завышенной: с точки зрения статистики разумно допустить не более чем 5% ошибку хрониста, которой на графике соответствует уровень значимости коэффициента, при данном числе максимумов равный 10 −16.

Обобщая вышесказанное, мы делаем вывод: «малые значения» коэффициента вытекают из самой его структуры (в частности сверхчувствительности к отклонениям), и еще не обеспечивают достоверности результата .

4) Наконец, мера близости оказывается не транзитивной, т.е. если точка X близка к точке Y , а точка Y — к точке Z , но в общем случае не всегда точка X близка к Z . Покажем это для коммутативных коэффициентов. Рассмотрим три «хроники» X , Y и Z , которые а) лежат на одной прямой в n -мерном пространстве, б) достаточно близко друг к другу и «глубоко» внутри множества Ш , чтобы их коэффициенты коммутировали, и в) так, что расстояния между X и Y и расстояния между Y и Z одинаковы и равны ρ. Поскольку точки лежат на одной прямой, то тогда расстояние между X и Z будет равно 2ρ.

Для коммутативных коэффициентов имеем Л ( X , Y ) = Л ( Y , Z ) = ε, где ε вычислено по формуле (8'). Мы можем положить, например, ε = 10 −8, и тогда хроники X , Y и Y , Z интерпретируются как «заведомо зависимые» (при числе максимумов от 10 до 15). Но, подставляя в (8')расстояние между точками X и Z , равное 2ρ, получаем

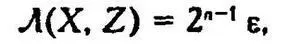
что дает, скажем, в нашем модельном примере при 14 максимумах (n=15):

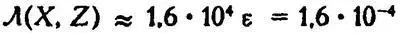
Итак, мера между X и Z отличается от меры точек-соседей более чем в 10 тысяч раз! Хотя пары X , Y и Y , Z считаются «заведомо зависимы», оценка связи X и Z находится далеко выше границы зависимых хроник, и приближается к значениям независимых. Отметим, что сам автор не только не оговаривает эти проблемы, но даже в своей книге неявно пользуется транзитивностью коэффициента, например, рассуждая о возможности продолжить книгу Тита Ливия учебником В. С. Сергеева (см. ниже). [253] Приведенный пример еще раз показывает, что основные "неприятности" коэффициента Л(X, Y) возникают из-за того, что мера, предложенная автором, получена с помощью возведения евклидового расстояния ?(X, Y) между точками в некую "большую" степень. Между тем, это расстояние само по себе уже служит мерой близости точек, и для него выполняются свойства коммутативности и транзитивности ("неравенство треугольника"), математически это означает, что ? (X, Y) является метрикой пространства R n . Мера же Л(X, Y), как мы показали, не является метрикой, именно поэтому в ее интерпретации как статистического коэффициента заключены серьезные проблемы.