Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

У вас появились какие-нибудь идеи? Если нет, читайте дальше.

Я надеюсь, что за то время, которое мы провели за разговором о факториалах, вы приблизились к решению. Нет никаких сомнений, что факториалы играют в нем какую-то роль. Но какую?

С какого числа следует начать? Может быть, с 100!? Нет, этот вариант не годится. Ведь следующее число, 100! + 1, вполне может оказаться простым, не так ли?

А вот если… Вы уже видите решение?

Может быть, начать с 100! + 2? Такая идея кажется более привлекательной. Это число делится на 2, поскольку на 2 делятся и 100! и 2; следовательно, оно не может быть простым. Мы на верном пути.

Следующее число, 100! + 3, точно так же делится на 3, и, если продолжать в том же духе… 100! + 100 делится на 100. К сожалению, мы никак не можем немедленно установить, составное ли число 100! + 101.

Решение было так близко. Но увы, между 100! + 2 и 100! + 100 всего 99 чисел. Как жаль! Такая прекрасная идея отправляется в помойку.

Минуточку! В помойку? Ни в коем случае! Ее всего лишь нужно немножко подправить.

Мы можем начать свою последовательность чисел с 101! + 2 и закончить ее на 101! + 101. Тогда мы получим непрерывную последовательность из 100 идущих друг за другом чисел, и все они, вне всякого сомнения, – числа составные.

Очевидно, теперь мы можем найти последовательность чисел любой длины, в которой не будет ни одного простого числа. Например, чтобы получить набор из 1000 последовательных составных чисел, нужно просто начать эту последовательность с 1001! + 2. Из этого, разумеется, следует, что среди по-настоящему больших чисел простые числа будут встречаться все реже и реже {15} 15 Теорема о распределении простых чисел утверждает (более или менее) следующее: вероятность того, что число, близкое к n , окажется простым, пропорциональна натуральному логарифму n , деленному на n . Поскольку это отношение стремится к 0 при n , стремящемся к бесконечности, это гарантирует редкость появления простых чисел среди всех натуральных чисел. .

По мере увеличения чисел средняя разность двух последовательных простых чисел тоже становится больше. Однако существует теорема, которая устанавливает верхний предел редкости появления простых чисел среди чисел натуральных. Она утверждает, что отношение

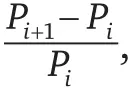
где P i – значение i -го простого числа, приближается к нулю по мере приближения i к бесконечности.

Я переведу это утверждение с математического жаргона на язык понятный и нематематикам. Теорема эта означает, что отношение длины промежутка между простыми числами к самим простым числам становится меньше с увеличением i . Ниже приведен список значений начиная с i = 1. Чтобы было яснее, уточню, что в первой строке i равно 1; следовательно, P i – это первое простое число, то есть 2, а P i +1 – второе простое число, то есть 3. Во второй строке i = 2, а простые числа – P 2 = 3 и P 3 = 5 и так далее.

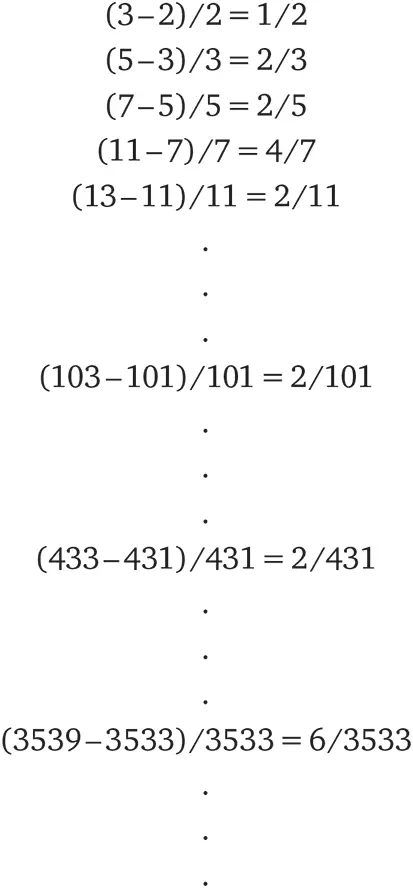
Как вы видите, значение выражения

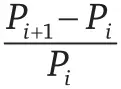
имеет тенденцию становиться все меньше и меньше по мере увеличения i (значение этого выражения не уменьшается монотонно; оно лишь проявляет общее снижение с ростом P ), потому что при больших простых числах его числитель становится много меньше знаменателя. Это означает, что разность последовательных простых чисел (чисел, стоящих в числителе) растет медленнее, чем значения самих этих чисел, что и приводит к уменьшению отношения. Хотя в первых строках списка есть некоторая нестабильность, если рассмотреть общую тенденцию, можно увидеть, что промежутки между простыми числами становятся все меньше по сравнению с самими этими числами.

Несмотря на многолетние исследования, аспектов простых чисел, которых мы не понимаем, все еще гораздо больше, чем понятных нам.

Вот лишь некоторые из (множества) задач, которые, насколько мне известно, до настоящего времени никто не решил. Может быть, вы захотите попытаться найти их решение. Могу вам гарантировать, что, если вы решите даже одну из них, вы немедленно получите докторскую степень по математике и прославитесь. А если вы еще учитесь в школе или университете, решение этих задач принесет вам полное освобождение от всех дальнейших уроков или лекций. Таковы хорошие новости.

Плохие же новости по-настоящему плохи. В том, что никому до сих пор не удалось решить эти задачи, нет ничего случайного. Они исключительно сложны! Трудно представить себе, сколько усилий математики потратили на попытки их решить. «Бесплатных завтраков не бывает», – говорят нам наши экономисты. Я бы еще добавил к этому, что «не бывает и роскошных банкетов, которые обходились бы дешево».

Два простых числа считают близнецами, если их разность равна 2. Например, пары (3, 5), (5, 7), (11, 13), …, (431, 433)… – это пары чисел-близнецов.

Бесконечно ли количество простых чисел-близнецов?

Из одного того, что количество простых чисел бесконечно, не следует, что ответ на этот вопрос должен быть утвердительным.

Перед вами триплет простых чисел {16} 16 Триплет простых чисел – это набор из трех простых чисел вида ( p, p + 2, p + 6) или ( p, p + 4, p + 6). Это самое тесное из возможных расположений трех простых чисел, так как одно из любых трех последовательных нечетных чисел оказывается кратно трем и, следовательно, не является простым (за исключением самого числа 3) – кроме случаев (2, 3, 5) и (3, 5, 7). : (3, 5, 7). Докажите, что это единственная возможная «тройка близнецов».

Пары простых чисел, разность которых равна 4, – например (3, 7), (7, 11), (19, 23), …, (223, 227), – называют двоюродными простыми числами или кузенами. Бесконечно ли количество таких пар?

Пары простых чисел, отличающихся на 6, называются по-английски sexy primes [20] По совпадению латинского слова sex (шесть) со словом «секс» в современных языках. Заметим, что в латыни это слово, по-видимому, не имело никакого отношения к полу ( sexus ). , то есть «сексуальными простыми числами». Ну и представления о сексуальности у этих математиков! Вот некоторые из победителей на конкурсе самых сексуальных пар: (5, 11), (7, 13), (11, 17), (17, 23), (23, 29), …, (191, 197)…