Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Тот факт, что количество простых чисел бесконечно, означает, что мы никогда не сможем составить полный список всех простых чисел. Всегда будет оставаться следующее простое число, большее, чем самое большое число в нашем списке.

Число, носящее почетный титул «самого большого простого числа, открытого до 2018 г.», равно 2 77 232 917 – 1 [17] В декабре 2018 г. было найдено еще большее простое число Мерсенна, равное 2 82 589 933 – 1. В десятичной записи оно содержит 24 862 068 цифр. К моменту выхода настоящего издания вполне могут устареть и эти сведения. . Я не советовал бы вам пытаться сосчитать это число и выписать его в тетради: в ней просто не хватит для этого страниц. Если учесть, что количество атомов во Вселенной меньше, чем 2 320, наверное, можно составить некоторое представление о том, насколько огромно число 2 77 232 917 – 1. В нем 23 249 425 знаков – почти на миллион (!) больше, чем в числе, которое считалось самым большим простым числом до него: то было открыто в январе 2016 г., и его значение – 2 74 207 281 – 1 (в этом числе «только лишь» 22 338 618 знаков). При этом число 2 320 всего-то 96-значное. Все относительно!

Кстати говоря, доказательство того, что это чудовищное число относится к простым числам, было получено не живым математиком из плоти и крови, а сетевым вычислительным проектом под названием GIMPS (Great Internet Mersenne Prime Search – «Великий интернет-поиск простых чисел Мерсенна»).

Что же такое «число Мерсенна»? Возможно, правильнее было бы спросить иначе: кто такой Мерсенн? Числа вида 2 n – 1 называют числами Мерсенна в честь французского философа, богослова, музыковеда и математика Марена Мерсенна (1588–1648). Если вам кажется, что перечень его титулов недостаточно впечатляющ, позвольте мне добавить еще один: Мерсенн был первым человеком, измерившим скорость звука.

Все ли числа Мерсенна простые? Вовсе нет.

Например, 2 4 – 1 = 15 – не простое число (15 = 3 × 5).

Те, кто еще не забыл уроки старших классов (или, скажем, все еще учится в школе), вероятно, знают, что число Мерсенна не относится к простым, если простым числом не является его степенной показатель. Дело в том, что в этом случае такое число всегда можно разложить на два сомножителя. Механизм, лежащий в основе этого правила, любезно вызвалось проиллюстрировать на собственном примере число 2 6 – 1:

2 6 – 1 = 2 2 × 3 – 1 = (2² – 1) (2 4 + 2 ² + 1) = 3 × 21 [18] Или, если использовать формулу разности квадратов, 2 3 × 2 – 1 = (2³ – 1) (2³ + 1) = 7 × 9. .

Другими словами, если степенной показатель – составное число, то соответствующее число Мерсенна всегда можно разложить на множители, что доказывает, что и оно будет числом составным. Для его разложения есть общая формула:

2 n · m – 1 = (2 n – 1) (1 + 2 n + 2² n + … + 2 ( m – 1) · n ).

Если эта формула не кажется вам особенно интересной, не беспокойтесь. Собственно говоря, сама формула не столь важна. Важен тот факт, что если в степенном показателе стоит не простое число, то и число Мерсенна с этим показателем не будет простым. Но если составной показатель гарантирует составное число Мерсенна, дальше, несомненно, естественно задать следующий вопрос: «Гарантирует ли простой показатель, что число Мерсенна будет простым?»

Попробуем проверить.

2² – 1, 2³ – 1, 2 5 – 1 и 2 7 – 1 – числа простые (соответственно 3, 7, 31 и 127). Пока что все хорошо. Сле- дующее простое число после 7 – это 11, но 2 11 – 1 – это не простое число: 2 11 – 1 = 2047 = 23 × 89.

Как ни печально, наличие простого числа в степенном показателе не гарантирует, что соответствующее число Мерсенна тоже будет простым числом. Будь это так, мы бы располагали простым способом находить все новые и новые простые числа. Например, можно было бы взять то колоссальное простое число, о котором мы говорили несколькими строчками выше, использовать его в качестве степенного показателя 2, вычесть единицу и получить новое – и еще более колоссальное – простое число. В его показателе стояло бы число, содержащее более 20 миллионов цифр. Подумайте только, каким ужасающе огромным было бы это число – оно выходило бы за пределы воображения простых смертных. Простое ли это число на самом деле? Я этого не знаю и не думаю, что когда-нибудь узнаю.

Мерсенн исследовал эти числа, носящие теперь его имя, в работе, опубликованной в 1644 г. Она вышла под величественным заголовком «Физико-математические размышления» (Cogitata Physico-Mathematica). Мерсенн проверил все простые степенные показатели до 257 и заключил, что числа вида 2 P – 1 должны быть простыми при P = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257. Правильный перечень немного отличается от этого и выглядит так: P = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127.

Судите сами, можно ли считать процент точных попаданий Мерсенна впечатляющим.

Помните совершенные числа, с которыми мы познакомились в разделе, посвященном Пифагору? Если вы уже забыли про них, напомню, что совершенным называется число, сумма собственных делителей которого равна самому числу. Еще Евклид знал, что, если 2 P – 1 – простое число, то его умножение на 2 P – 1всегда дает совершенное число. Разумеется, Евклид не называл такие числа числами Мерсенна. В его время не только еще не родился сам Мерсенн, но даже не познакомились родители прародителей его прародителей.

Приведем несколько примеров. 2³ – 1 – простое число (7); следовательно, (2³ – 1) × 2² = 28 – число совершенное. Аналогичным образом, 2 5 – 1 – простое число (31); следовательно, (2 5 – 1) × 2 4 = 496 – число совершенное. Воспользовавшись любезной помощью наибольшего из известных на сегодня простых чисел, мы теперь можем построить и самое большое из известных совершенных чисел: (2 77 232 917 – 1) × 2 77 232 916.

Я не советовал бы вам пытаться сосчитать это число и проверить справедливость этого утверждения. Могу вас заверить, что сумма всех делителей этого чудовищного числа действительно равна самому числу. Говоря словами великого немецкого философа Иммануила Канта, мне пришлось устранить знание, чтобы дать место вере.

Ну хорошо. Теперь настало время отвлечься от мировых рекордов и заняться разработкой некоторых из пресловутых умственных мускулов.

1). Докажите, что, если 2 P – 1 – простое число, то число (2 P – 1) × 2 P – 1должно быть совершенным.

2). 28 – треугольное число.

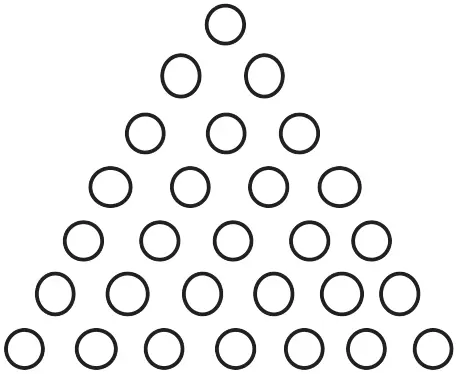
Являются ли все совершенные четные числа треугольными?

Знаменитый швейцарский математик Леонард Эйлер (с которым мы вскоре познакомимся) доказал, что верно и обратное. Другими словами, любое четное совершенное число имеет форму (2 P – 1) × 2 P – 1, где P и 2 P – 1 – простые числа. Попробуйте свои силы и докажите это утверждение – или же найдите доказательство Эйлера {14} 14 Подсказка: Найдите наибольшую степень 2, на которую делится ваше число. Ее и следует взять в качестве P – 1. .