Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Число, имеющее бесконечное десятичное представление с повторяющейся структурой также рационально, хотя понять это может быть немного труднее. Например, рассмотрим число r = 0,123123123123… В этом числе имеется простая повторяющаяся структура, и легко доказать, что это число рационально, то есть может быть представлено в виде a / b .

Умножим число r на 1000 (число 1000 было выбрано в связи с длиной повторяющейся структуры) и вычтем из результата r :

1000 r – r = 999 r = 123,123123123… – 0,123123123… = 123.

Следовательно, r = 123/999, что можно сократить до 41/333, а это явное отношение двух целых чисел, и, если вы разделите в столбик 41 на 333, вы сможете убедиться, что эта дробь действительно равна 0,123123123…

Однако проделать тот же фокус с √2 нельзя, потому что десятичное представление этого числа бесконечно и не повторяется. Мы можем найти дроби, очень близкие к √2, – например 577/408. Они дают весьма хорошее приближение, но и только – всего лишь приближение . Интересно отметить, что сам Пифагор отказывался считать √2 числом. Многие упрекали – и до сих пор упрекают – его за это; на мой взгляд, безосновательно.

Важно помнить, что √2 – всего лишь символ числа, которое при умножении само на себя дает 2. Как я уже говорил, можно было выбрать символом этого числа не √2, а цветок, и сказать, что этот цветок обозначает число, при возведении которого в квадрат получается 2. Отличается ли общепринятый математический символ от цветка? Может быть, нам следовало бы начать использовать в математике побольше цветов – тогда она стала бы гораздо более веселой.

Единственное различие между общепринятым символом и нашим цветком состоит в том, что цветок менее удобно использовать. На самом деле нас вообще не интересуют символы: мы хотим записать число, квадрат которого равен 2. Но оказывается, что сделать этого мы не можем: сколько бы цифр после запятой мы не выписали, их никогда не будет достаточно. Нам нужно выписать бесконечно много цифр, а этого не случится никогда.

Феодор (465–398 до н. э.), родившийся лет через тридцать после смерти Пифагора и бывший личным учителем математики у Платона, доказал, что квадратные корни из 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 и 17 также равны иррациональным числам. Платон восхищался Феодором и даже упомянул его открытие иррациональности квадратных корней в диалоге «Теэтет» {19} 19 «Теэтет» – один из диалогов Платона, посвященных природе знания. Он был написан около 369 г. до н. э. . Мнения о том, почему он остановился на 17, разнятся. В диалоге Теэтет просто говорит Сократу, что Феодор остановился на этом числе. Популярная версия утверждает, что Феодор строил из треугольников спиральную конструкцию, которая носит сегодня его имя. Если вы продолжите это построение, то сразу же увидите, почему его последовательность прекратилась именно на этом числе. Вот спираль Феодора:

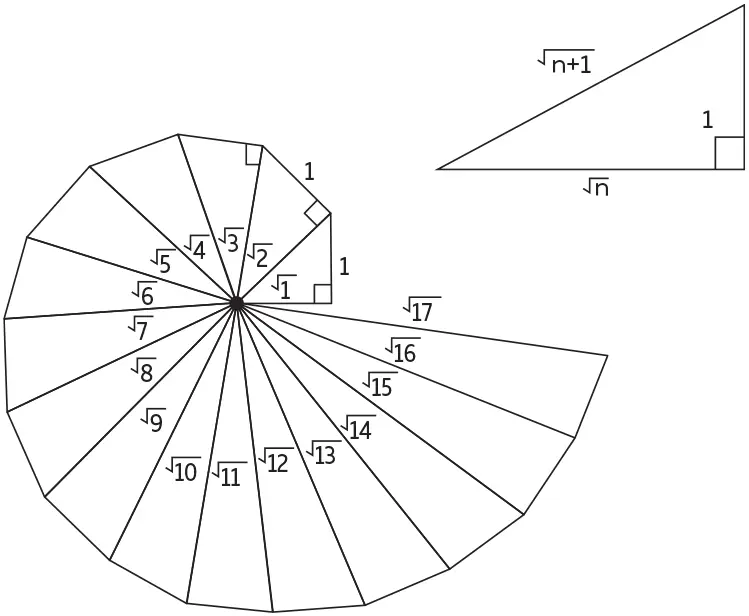
Докажите, что квадратный корень из 3 – иррациональное число.

Попробуйте доказать, что квадратный корень из любого целого числа может быть только либо целым, либо иррациональным числом. Другими словами, квадратный корень из любого целого числа, кроме полного квадрата – 4, 9, 16, 25 и так далее, – всегда иррационален.

Ну хорошо. Когда Пифагор решил, что на свете не существует числа, квадрат которого равен 2, он слегка преувеличивал. На свете есть число, квадрат которого равен 2, и число это иррационально. Сегодня математики умеют обращаться с такими числами без особых затруднений – даже несмотря на то, что мы не можем записать их полностью. Честь основания математической теории иррациональных чисел в первую очередь следует приписать трем математикам – Рихарду Дедекинду (1831–1916), Карлу Вейерштрассу (1815–1897) и Георгу Кантору (1845–1918). Не следует полагать, что работать с такими числами легко и просто. Подумайте, например, как сложить √2 и √3 – притом что оба эти числа имеют бесконечное десятичное представление.

В самом деле, как сложить 1,41421356237309504880168872420969807… и 1,73205080756887729352744634150587236…?

Фундаментальные правила сложения, которым нас научили еще в школе, гласят, что начинать надо со сложения самых правых цифр. Но здесь мы не можем найти самые правые цифры – десятичное представление этих чисел бесконечно! Что же делать? Я же говорил вам, что не следует насмехаться над Пифагором из-за того, что он не желал считать иррациональные числа числами.

Многие считают сделанное Пифагором открытие иррациональных чисел самым важным открытием во всей истории математики {20} 20 Помимо того, что Пифагор открыл иррациональные числа, он внес еще один важный вклад в развитие математической науки: он ввел концепцию «доказательства» в смысле, очень похожем на тот, что известен нам сейчас. .

Легенда утверждает, что Пифагор велел своим ученикам хранить его открытие иррациональности длины диагонали квадрата относительно длин его сторон в секрете. Однако один из них, Гиппас, нарушил данное ему обещание (неизвестно, по каким причинам – научным или политическим) и разгласил эту тайну. Далее легенда рассказывает, что Гиппас был изгнан из сообщества пифагорейцев, а кое-кто утверждает даже, что его утопили в море (он попросту не вернулся из одного из своих плаваний вокруг греческих островов). По другой версии, иррациональные числа открыл именно Гиппас, а Пифагор не имел к этому открытию никакого отношения.

Более чем через две тысячи лет после смерти Пифагора Кантор показал, что «почти» все вещественные числа иррациональны. В число таких чисел входят и два из самых важных чисел в математике – число Эйлера e и отношение длины окружности к ее диаметру, число π.

Я обещал, что буду использовать в этой книге только четыре базовые математические операции. Но кому нужен такой «закон», который нельзя нарушить хотя бы один раз? Вот сейчас мы его и нарушим.

Числа, доказать иррациональность которых легче всего, порождаются операцией логарифмирования {21} 21 Если вы вдруг забыли, что такое логарифм, напомню, что логарифм – это функция, обратная показательной. То есть если b y = x , то log b x = y . Другими словами, логарифм данного числа x – это степень, в которую нужно возвести другое данное число, основание b , чтобы получить число x . Например, 1000 = 10³; следовательно, log 10 1000 = 3. Точно так же log 2 64 = 6, поскольку 2 6 = 64. . Например, рассмотрим log 23, то есть логарифм 3 по основанию 2. Докажем его иррациональность. Для начала предположим, что этому числу равно отношение m / n :

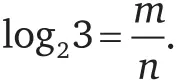
Исходя из определения логарифма и законов операций со степенями, из этого следует, что 2 m / n = 3, а (2 m / n ) n = 3 n , а следовательно, 2 m = 3 n .