Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Однако никакая степень 2 не может быть равна какой бы то ни было степени 3 [28] Напомним, что речь идет о степенях, являющихся натуральными числами. – Примеч. ред. : 2 в любой степени всегда дает четное число, а 3 в любой степени – нечетное. Значит, мы пришли к противоречию. Другими словами, не существует таких чисел m и n , для которых

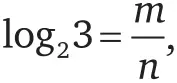
что означает, что m / n не может быть рациональным. Следовательно, log 23 – иррациональное число.

1. Докажите, что золотое сечение {22} 22 Две величины образуют золотое сечение, если их отношение равно отношению их суммы к большей из них (то есть если a > b и a / b = ( a + b )/ a , то величины a и b образуют золотое сечение). Золотое сечение обозначают буквой ϕ. ϕ [29] В русской математической литературе это число чаще обозначают прописной буквой Φ, а строчной буквой ϕ – число, обратное ему, т. е. 1/Φ. – иррациональное число.

2. Символом секты пифагорейцев была пентаграмма, вписанная в пятиугольник.

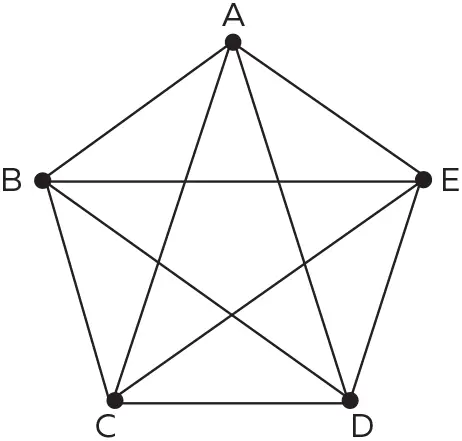
Докажите, что отношение длины диагонали правильного пятиугольника к длине одной из его сторон иррационально. Покажите также, что это отношение равно не произвольному иррациональному числу, а числу ϕ (см. предыдущую задачу). Другими словами, отношение любой диагонали этой фигуры к любой ее стороне равно золотому сечению!

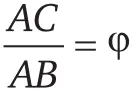
Как же повезло Пифагору, что он так и не узнал, что эти нахальные иррациональные числа, которые он не желал считать равноправными членами семейства чисел, скрывались даже в его собственной эмблеме!

Пифагорейский символ можно дополнить следующим образом:

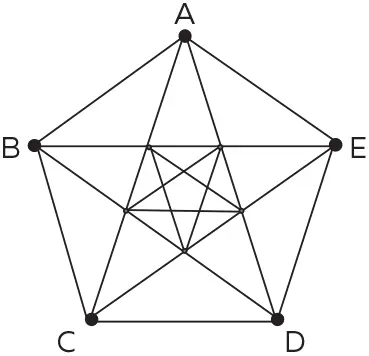
И такие «дополнения» можно продолжать до бесконечности!

1. Рационально ли число 0,07007000700007…?

2. Рационально ли число 0,123456789101112…?

3. А как насчет числа 0,01123581321345589144…, образованного из членов последовательности Фибоначчи – 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55… (эта последовательность начинается с 0 и 1, после чего каждый следующий член равен сумме двух предыдущих)?

Страх бесконечности, присущий древним грекам, замечательно выражается в знаменитых апориях [30] Апория ( греч . ἀπορία) – вымышленная, логически непротиворечивая ситуация, которая не может существовать в реальности. Построения Зенона принято называть по-русски именно апориями, а не парадоксами. Зенона Элейского, родившегося около 490 г. до н. э. Он в основном работал в Греции [31] Уточним, что речь идет не о Греции в современных границах, а о всем комплексе городов и колоний греческой культуры, которые существовали в Античности в разных районах Средиземноморья, от Малой Азии до Прованса. В частности, город Элея находился в нынешней Кампании на юге Италии, километрах в ста от Неаполя. около 450 г. до н. э. О жизни Зенона известно мало. По-видимому, он провел большую ее часть на родине, в городе Элее, хотя Платон рассказывает нам в диалоге «Парменид» об интереснейшей встрече в Афинах, на которой присутствовали Зенон, Парменид и молодой Сократ.

Первоисточник Зенона не сохранился, и исследователи по большей части ссылаются на Аристотеля, который пересказывает апории Зенона в своей «Физике».

Зенон создавал свои апории на основе философии своего учителя и друга Парменида. Поэтому, прежде чем мы перейдем собственно к апориям Зенона, давайте узнаем кое-что о Пармениде и его необычной философии.

Парменид, учитель и друг Зенона (Платон намекал даже, что Зенон с Парменидом были любовниками [32] Об этом пишет и Диоген Лаэртский (IX, 5). ), считается явлением исключительным не только в греческой философии, но и во всей истории западной философии. Единственная известная работа Парменида «О природе», написанная в форме поэмы, дошла до нас лишь в отрывках. Парменид описывает два взгляда на реальность: «путь истины» и «путь чувств». Говоря о «пути истины», он объясняет, что реальность безвременна, однородна, бесконечно плотна и неизменна. Говоря о «пути чувств», он объясняет мир кажущегося и мнений, ложный и обманчивый. Жизненная философия Парменида состояла в том, что мир чувств – всего лишь иллюзия, а истинная Вселенная, которую можно познать только путем строгих размышлений, безмолвна и неподвижна. Он утверждал, что истинная Вселенная находится сейчас точно в том же состоянии, в котором она находилась секунду назад, год назад, миллиард лет назад, – и пребудет в нем же вовеки.

Что??? Это утверждение кажется несусветным даже для греческого философа.

Вот в чем заключалась суть его философии и каким образом он к ней пришел.

Парменид искал истины столь очевидной, что любые сомнения относительно ее справедливости были бы невозможны. Он хотел положить такую несомненную истину в основу всей своей философии. В математике такая истина называется аксиомой. Проведя много дней в утомительных размышлениях, Парменид заснул, и во сне ему явилась Афина – богиня мудрости, дочь Зевса и покровительница города Афин, – которая и помогла ему найти то, что он искал: То, что есть, есть, а того, чего нет, нет .

То есть Парменид утверждает, что существующее есть, а несуществующего нет. Это утверждение кажется очевидным и неопасным. Вы уверены? Тогда читайте дальше.

Вооружившись этой аксиомой, Парменид сформулировал несколько новых истин (на языке математики они называются теоремами). Сперва он предложил Первую теорему Парменида:

Существующее (то, что есть) не могло быть создано и не может исчезнуть.

Эта теорема доказывается почти мгновенно. В математике мы называем этот метод (как уже было упомянуто в другом месте) «доказательством от противного»: мы предполагаем, что справедливо обратное утверждение – что «то, что существует» когда-то было создано, – и проверяем, приводит ли это к логическому противоречию. Если приводит, это означает, что исходное предположение было неверным.

Если «то, что существует» было создано, оно должно было быть создано из чего-то, либо из того «что есть», либо из того «чего нет». Ничто не может быть создано из того «чего нет», потому что там ничего нет. Но, если «то, что существует» было создано из чего-то «что есть», это значит, что «то, что существует» уже существовало. Следовательно, «то, что существует» никогда не было создано.