Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Ч. т. д.

Предлагаю хитроумному читателю самостоятельно доказать аналогичным образом, что «то, что существует», никогда не может исчезнуть.

Затем философ доказал свою Вторую теорему Парменида:

Все существующее равномерно и бесконечно плотно.

Доказательство этого утверждения тоже поразительно просто. То, что существует, должно быть бесконечно плотным, потому что, если это не так, значит, оно содержит по меньшей мере некоторое количество «того, что не существует». Но «того, что не существует» не существует. Мнение Парменида, что «того, чего нет» нет, многократно истолковывалось в смысле отрицания пустоты. Пустота – это «то, чего нет», а следовательно, ее не существует.

Аналогичным образом все то, что существует, должно быть равномерное плотным, потому что, если есть нечто, что существует и обладает меньшей плотностью, это значит, что в нем больше «того, что не существует». Но «того, что не существует» не существует!

Опять же ч. т. д.

Вам уже кажется, что происходит нечто странное? То ли еще будет!

Доказательство этого утверждения совершенно очевидно: если все бесконечно плотно, как может быть возможно движение?

Тот факт, что мало кто отрицает существование движения, Парменида совершенно не заботил. Его не интересовал мир чувств и мнений, в котором существует возможность ошибки. В его мире истины (мире аксиом и теорем) все неподвижно, ничто не создается и ничто не исчезает.

Вернемся к Зенону. В той единственной книге, которую он, по-видимому, написал, он пытался защищать философию своего наставника. В частности, он хотел подкрепить утверждение Парменида относительно невозможности движения – утверждение, за которое Парменида больше всего критиковали, если не сказать высмеивали. И действительно, верить, что движения не существует, – занятие очень странное.

Защищая своего учителя, Зенон изложил свои знаменитые апории, которые увлекают бесчисленных математиков и философов вот уже более двух тысяч лет. В число тех, кто всерьез размышлял над ними, пытаясь понять, входят Аристотель, Маймонид, Декарт, Лейбниц, Спиноза, Бергсон, Рассел, Льюис Кэрролл, Кафка, Сартр, Гегель и Ленин (который прочитал об апориях в книге Гегеля и написал в своих «Философских тетрадях», что они совсем неплохи) – а также многие, многие другие.

Что же это за апории?

Первая апория называется «Дихотомия», и в ней Зенон демонстрирует невозможность движения при помощи чрезвычайно рационального и логичного объяснения.

Посмотрите на приведенный ниже чертеж. Зенон утверждает, что, чтобы попасть из точки А в точку В , необходимо пройти расположенную посередине между ними точку С .

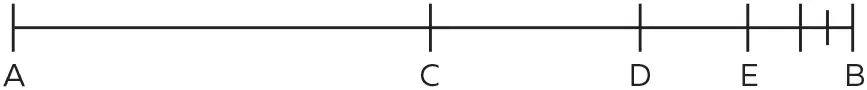
Но, чтобы попасть из С в В , необходимо сначала пройти половину расстояния между ними и добраться до точки D . Однако и попав в эту точку, особо радоваться не следует, так как, чтобы добраться из нее до точки В , теперь необходимо сначала преодолеть половину оставшегося расстояния и попасть в точку Е . И так далее и так далее.

Вот рассуждение Зенона: «Невозможно пройти бесконечное число точек за конечное время. Следовательно, попасть из точки А в точку В вообще невозможно». Наконец-то мы понимаем, как решить задачу, в которой спрашивается «сколько времени понадобится поезду, чтобы прибыть в одну точку, после того, как он выйдет из другой точки?». Правильный ответ – этот поезд никогда никуда не придет. А поскольку точки А и В выбраны совершенно произвольно, отсюда следует, что переместиться из любого места в любое другое также невозможно. Следовательно, невозможно и движение.

Во множестве книг излагается разрешение этого противоречия. Рассуждение движется (Зенон резко возражал бы против использования слова «движется») более или менее по следующему пути: предположим, что время, необходимое для преодоления определенного расстояния, пропорционально его величине. Тогда мы можем доказать, что Зенон был неправ, потому что все бесконечные «половинные расстояния» (которые становятся все меньше и меньше) можно преодолеть за конечное время. Например, если предположить, что перемещение из точки А в точку С занимает в точности одну единицу времени – скажем, минуту, – то перемещение из точки С в точку D займет полминуты (поскольку это расстояние равно половине предыдущего), из точки D в точку Е – четверть минуты и так далее. Обозначим суммарное время, требуемое для перемещения из А в В, буквой S:

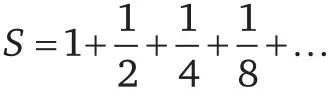
Разделив обе части на 2, получим:

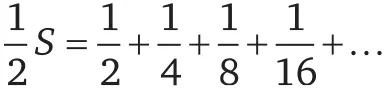
Вычтем второе равенство из первого:

.

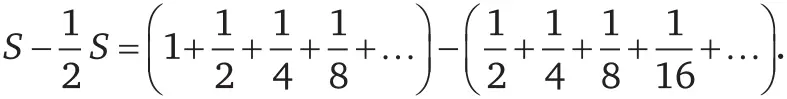
Следовательно,

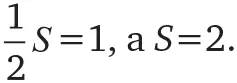
Другими словами, преодоление бесконечного числа серединных точек между А и В займет ровно две минуты.

Честно говоря, этот ответ не так уж и удивителен. Мы начали с предположения, что одну минуту занимает перемещение от А до С , то есть ровно на половину суммарного расстояния; поэтому никого не должно удивлять, что все это расстояние преодолевается за две минуты.

Зенон, несомненно, возражал бы против такого решения самым энергичным образом, потому что мы получили его, предположив именно то, что нужно было доказать. Когда мы сказали «если предположить, что перемещение из точки А в точку С занимает одну минуту», мы уже предположили, что движение возможно и из точки А можно переместиться в точку С . Однако именно это положение и нужно доказать, и, следовательно, наши рассуждения образуют так называемый порочный круг.

Зенон, вероятно, пояснил бы свою точку зрения, сказав что-нибудь вроде: «Как и на каком основании вы предполагаете , что из точки А можно попасть в точку С ? Мне совершенно очевидно, что вы совершаете гигантскую ошибку. Ясно, как солнце летним днем на прекрасном греческом острове, что, прежде чем попасть из точки А в точку С , необходимо преодолеть половину расстояния между ними и достичь точки Х . После этого нужно преодолеть половину оставшегося расстояния до С и добраться до точки Y и так далее и так далее.