Агниджо Банерджи - Эта странная математика. На краю бесконечности и за ним

В отличие от ленты Мёбиуса, у бутылки Клейна нет краев или границ, что роднит ее со сферой. Но в отличие от сферы, у бутылки Клейна нет внутренней и внешней стороны – они идентичны, – поскольку она представляет собой единую поверхность, переходящую саму в себя. В реальном мире мы с подобным обычно не сталкиваемся. Нам привычнее объекты вроде банок с бочонками или бутылок с божоле, имеющие четко определенные внутреннюю и внешнюю стороны, а значит, заключающие в себе определенный объем. Но поскольку бутылка Клейна не разделяет пространство на две различных области, то она ничего в себе и не заключает, а стало быть, ограничивает нулевой объем.

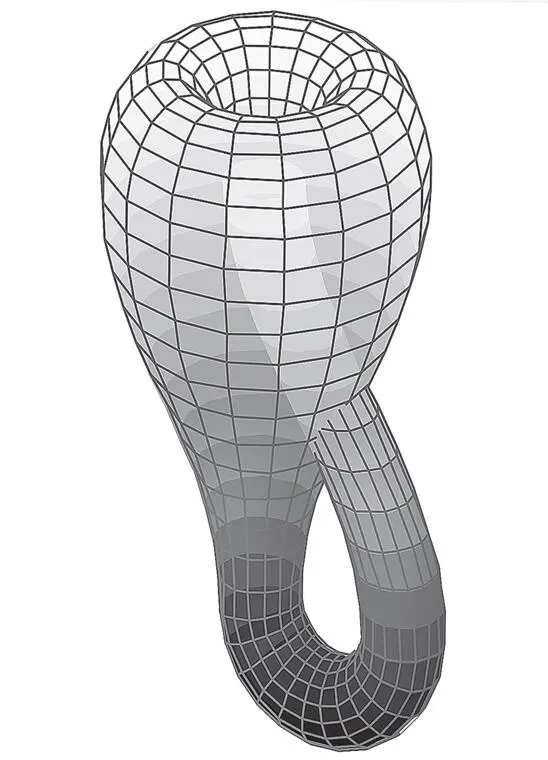
Бутылка Клейна, погруженная в три измерения. Ее “внутренняя” и “внешняя” стороны на деле неразличимы. Обычными способами этого не добиться – ее невозможно вложить в трехмерное пространство, – поэтому в нем поверхность бутылки Клейна пересекает саму себя.

И сферы, и торы, и ленты Мёбиуса – все это примеры двумерных поверхностей, которые можно “вложить” в трехмерное пространство. У термина “вложение” есть строгое математическое определение, но, если по-простому, это все равно что поместить одно пространство внутрь другого, отличного от него. Важно помнить, что сферы, ленты Мёбиуса, бутылки Клейна и другие геометрические объекты – это все абстракции, свойства которых никак не зависят от пространства, в котором они находятся: от того, сколько в нем измерений, плоское оно или искривленное и так далее. Но кое-что при вложении в разные пространства все же меняется. Например, тор можно вложить в три измерения (именно в таком виде мы с ним обычно и сталкиваемся), и тогда у него появляются отверстие – настоящее, математическое отверстие – и внешняя и внутренняя стороны.

Кое-кто из читающих эту книгу, возможно, еще помнит автоматы с классической игрой “Астероиды”. Управляя космическим кораблем, игрок должен сбить как можно больше пролетающих мимо него астероидов и летающих тарелок. Казалось бы, ничего общего со знакомым бубликом-тором. Но топологически они совершенно идентичны: и то и другое имеет тороидальную форму. Отверстие в бублике – это признак, появляющийся в результате погружения тора в три измерения, а вовсе не постоянное свойство всех торов. В “Астероидах” тороидальная топология пространства проявляется не в отверстии, а в том, как объекты, исчезающие с одной стороны экрана, тут же появляются с другой. Еще тор можно вложить в четырехмерное пространство. Одним из результатов такого вложения может оказаться тор Клиффорда, названный в честь жившего в Викторианскую эпоху математика Уильяма Кингдона Клиффорда (он, кроме прочего, впервые предположил, что тяготение – это следствие геометрии пространства, в котором мы живем). В отличие от хорошо известного нам тора-бублика с четко различимыми внешней и внутренней сторонами, тор Клиффорда не разделяет пространство, а потому ни внутренней, ни наружной стороны у него просто нет.

То же и с бутылкой Клейна. Австрийско-канадский математик Лео Мозер в форме лимерика описал, как родилась идея этой поверхности:

Потому у бутылки Клейна и нет краев: когда концы двух лент Мёбиуса (c правой и левой закруткой) соединяются вместе, образуется единая связная поверхность. Еще один способ сделать бутылку Клейна – начать с квадрата. Нужно соединить вместе пару его противоположных сторон, а потом в получившемся цилиндре состыковать вторую пару сторон, предварительно перекрутив одну из них на пол-оборота. Вот только этот второй шаг, хоть он и кажется простым, невозможно осуществить в трехмерном пространстве. Чтобы заставить поверхность пройти сквозь саму себя, не проделывая в ней отверстия, без четвертого измерения не обойтись. Впрочем, это мелкое затруднение не мешает энтузиастам изготавливать трехмерные модели, которые почти идеально (но все же не совсем точно) воспроизводят бутылку Клейна. Среди таких умельцев есть настоящие эксперты своего дела: например, Клиффорд Столл из Окленда (Калифорния, США), возглавляющий компанию Acme Klein Bottle , и Алан Беннетт из Бедфорда (Англия), который изготовил для лондонского Музея науки целую серию бутылок Клейна, аналогичных лентам Мёбиуса с нечетным числом оборотов больше одного. Математики называют подобные модели “погружениями” бутылки Клейна в трехмерное пространство. Погружение – не то же самое, что вложение. Не углубляясь в технические детали, скажем лишь, что в трехмерной модели (то есть при погружении) бутылки Клейна всегда будет место, где ее поверхность пересекает сама себя. Истинная же бутылка Клейна не имеет такого самопересечения, и его действительно не будет при ее вложении в четырехмерное пространство.

Другое важное свойство бутылки Клейна, да и любой другой поверхности, связано с ориентируемостью. Большинство поверхностей, с которыми нам приходится иметь дело в физическом мире, “ориентируемы”. Это значит, что если нарисовать на такой поверхности маленькую круговую стрелку, указывающую либо одно, либо другое направление, а потом двигать ее вдоль всей поверхности, пока она не вернется на исходное место, то по возвращении стрелка будет указывать прежнее направление. Так будет, к примеру, если взять сферу или тор: и то и другое – ориентируемые поверхности. А вот попробуйте-ка сделать то же самое с бутылкой Клейна или лентой Мёбиуса – и увидите, что, обойдя всю поверхность, стрелка-путешественница изменит направление на противоположное, поскольку эти поверхности неориентируемы.

Топологам приходится то и дело мысленно переключаться между пространствами разной размерности. Чтобы оперировать при этом некими общими понятиями, они изобрели для себя целый словарь специальных терминов. С “вложением” и “погружением” мы уже знакомы. Еще один – “многообразие”: это обобщение термина “поверхность” в приложении к другим измерениям. Все то, что мы называем “поверхностью”, по определению двумерно, поэтому правильно говорить не “двумерная поверхность” (это тавтология), а “двумерное многообразие”. Сфера, тор, лента Мёбиуса и бутылка Клейна – все это примеры двумерных многообразий. Первые три из них можно вложить в трехмерное пространство, а бутылку Клейна – нет. Прямые и окружности – это одномерные многообразия, а кроме них есть еще (хоть мы и не способны толком их себе представить) трехмерные многообразия, четырехмерные и так далее. Одно из простейших трехмерных многообразий – это трехмерная сфера. Подобно обычной двумерной сфере, которая представляет собой поверхность, ограничивающую шар в трехмерном пространстве, трехмерная сфера – это объект, имеющий три измерения и образующий границу четырехмерного шара. Мы не можем точно представить себе, как выглядел бы трехмерный аналог поверхности, не говоря уже о границах в более высоких измерениях. Но, несмотря на эту нашу ограниченность, у математиков есть весь инструментарий, необходимый им, чтобы оперировать подобными понятиями.