Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных

Байеса коэффициент:относительное подтверждение, которое дает какой-то набор данных двум альтернативным гипотезам. Для гипотез H 0, H 1и данных x это отношение равно p ( x | H 0)/ p ( x | H 1);

Байеса теорема:утверждение, которое показывает, как наступление события A изменяет наше априорное представление об утверждении B (априорную вероятность p ( B )) и дает апостериорное представление (апостериорную вероятность p ( B | A )) с помощью формулы 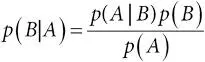. Ее нетрудно доказать: поскольку p ( BA ) = p ( AB ), то правило умножения для вероятностей означает, что p ( B | A ) p ( A ) = p ( A | B ) p ( B ), и деление обеих частей на p ( A ) дает утверждение теоремы;

байесовский подход:подход к статистическим выводам, при котором вероятность используется не только для стохастической, но и для эпистемической неопределенности в отношении неизвестных фактов. Затем с помощью теоремы Байеса можно пересмотреть представления в свете новых фактов;

Бернулли распределение:если X – случайная величина, которая принимает значение 1 с вероятностью p и значение 0 с вероятностью 1− p , то X имеет распределение Бернулли. Математическое ожидание (среднее) такой величины равно p , а дисперсия составляет p (1− p ). Сам эксперимент с двумя исходами (успех и неудача) называется испытанием Бернулли;

бинарные (двоичные) данные:переменные, которые могут принимать два значения, часто это ответы типа «да»/«нет» на какой-нибудь вопрос. Математически их можно представить с помощью распределения Бернулли;

биномиальное распределение:если у нас есть n независимых испытаний Бернулли с одной и той же вероятностью успеха, то число успехов в n испытаниях имеет биномиальное распределение. Формально: пусть X 1,…, X n – независимые случайные величины, имеющие распределение Бернулли с вероятностью успеха p . Тогда их сумма R = X 1 + X , +…+ X n имеет биномиальное распределение, при этом 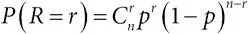, математическое ожидание (среднее) равно np , а дисперсия np (1− p ). Наблюдаемое отношение R / n имеет среднее p и дисперсию p (1− p )/ n . Поэтому величину R / n можно рассматривать как оценку для p со стандартной ошибкой ;

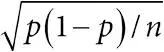большие данные:становящееся все более анахроничным выражение, которое иногда характеризуется четырьмя параметрами: большим объемом данных, разнообразием источников (изображения, аккаунты в социальных сетях, транзакции), большой скоростью получения и возможной нехваткой достоверности из-за шаблонных способов сбора;

Бонферрони поправка:метод для регулирования размера критерия (ошибка первого рода) или доверительных интервалов при одновременном тестировании многих гипотез. Более точно, при проверке n гипотез при общем размере критерия (ошибка первого рода) α каждую гипотезу проверяют с размером α/ n . Это эквивалентно тому, что для каждой оцениваемой величины указываются доверительные интервалы 100(1−α/ n )%. Например, если вы проверяете 10 гипотез с общим 5 %, то P-значения нужно сравнивать с 0,05/10 = 0,005 и использовать 99,5-процентные доверительные интервалы;

Бриера показатель:мера точности вероятностных прогнозов, основанная на среднеквадратичной ошибке прогноза. Если p 1,…, p n – это вероятности для двоичных наблюдений x 1,…, x n , принимающих значение 0 и 1, то показатель Бриера – это число 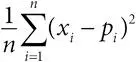. По сути, это критерий среднеквадратичной ошибки, примененный к бинарным данным;

бутстрэппинг:способ генерировать доверительные интервалы и распределения тестовых статистик путем создания повторных выборок из наблюдаемых данных, а не использования вероятностной модели для соответствующей случайной величины. Бутстрэп-выборка из набора данных x 1,…, x n – это выборка размера n с возвратом, так что хотя в нее попадают те величины, которые есть в исходной выборке, их доли в бутстрэп-выборке в целом будут отличаться от долей в исходной выборке;

вероятностное распределение:общий термин для математического закона, описывающего вероятность, с которой случайная величина принимает то или иное значение. Распределение величины X описывается функцией распределения F ( x ) = P ( X ≤ x ),−∞< x <���∞;

вероятностный прогноз:прогноз в виде вероятностного распределения для будущего события, а не категорического суждения о том, что оно произойдет;

вероятность:формальное математическое выражение неопределенности. Обозначим P(A) вероятность события A. Тогда справедливы такие правила для вероятности [277]:

1. 0 ≤ P(A) ≤ 1, при этом вероятность невозможного события равна 0, а достоверного – 1.

2. Вероятность противоположного (дополнительного) события Ā (которое заключается в том, что А не произошло): P(Ā) = 1 – P(A).

3. Правило сложения: если A и B – несовместные события (то есть произойти может только какое-то одно), то P(A или B) = P(A) + P(B).

4. Правило умножения: для любых событий A и B, P(A и B) = P(A|B)P(B), где P(A|B) означает вероятность события А при условии, что В произошло. А и В независимы тогда и только тогда, когда P(A|B)=P(A), то есть наступление события В не влияет на вероятность события А. В этом случае мы имеем P(A и B) = P(A)P(B) – правило умножения для независимых событий [278];

вероятность случайного совпадения:при судебной экспертизе ДНК – вероятность того, что человек, случайно выбранный из надлежащей популяции, будет соответствовать найденной ДНК в степени, которая связывает подозреваемого и преступление;

внешняя валидность:когда заключения исследования можно обобщать на целевую совокупность, которая шире, чем непосредственно исследуемая совокупность. Относится к релевантности исследования;

внутренняя валидность:когда заключения какого-либо исследования действительно касаются только изучаемой совокупности. Это относится к строгости, с которой проведено исследование;

воздействие:фактор, влияние которого на заболевание, смерть или иной медицинский исход, представляет для нас интерес, например какой-то аспект окружающей среды или поведения;