Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных

отсекаемый отрезок 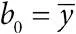. Прямая по методу наименьших квадратов проходит через центр тяжести ;

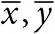i -й остаток – разность между i -м наблюдением и его предсказанным значением ;

скорректированное значение i -го наблюдения – это сумма остатка и отсекаемого отрезка, то есть 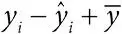. Это значение мы наблюдали бы в «среднем» случае, если бы имели 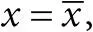а не x = x i ;

остаточная сумма квадратов – это сумма квадратов всех остатков, то есть 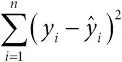. Прямая, построенная по методу наименьших квадратов, определяется как прямая, минимизирующая сумму квадратов разностей;

коэффициент наклона b 1и коэффициент корреляция Пирсона r связаны формулой b 1 = rs y / s x . Поэтому в случае, когда стандартные отклонения для x и y одинаковы, коэффициент угла наклона в точности равен коэффициенту корреляции;

множественная линейная регрессия:предположим, что для каждого отклика y i есть набор из p предикторных переменных ( x i 1, x i 2,…, x ip ). Тогда множественная линейная регрессия по методу наименьших квадратов определяется уравнением

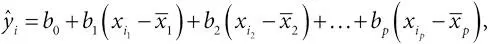
где коэффициенты b 0, b 1,…, b p выбираются так, чтобы минимизировать сумму остатков 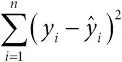. Отсекаемый отрезок b 0 – это просто среднее 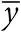, а формулы остальных коэффициентов сложны, но легко вычисляются. Обратите внимание, что 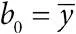является спрогнозированным значением наблюдения y , если предикторные переменные были средними 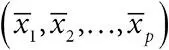, и, как в случае линейной регрессии, скорректированные определяются суммой остатка и отсекаемого отрезка, или ;

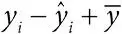многоуровневая регрессия и постстратификация (MRP):современный способ создания выборки, при котором из многих областей берутся достаточно небольшие количества респондентов с похожими характеристиками. Затем строится регрессионная модель для откликов в соответствии с демографическими факторами, что допускает дополнительный разброс между областями. Знание демографии для всех областей позволяет делать прогнозы на местном и национальном уровне с соответствующей неопределенностью;

множественная проверка гипотез:выполнение сразу нескольких проверок, что увеличивает вероятность получения хотя бы одного ложноположительного результата (ошибка первого рода);

мода (вероятностного распределения):для дискретного распределения – самое вероятное значение, для непрерывного – точка максимума плотности;

мода (выборки):значение, которое встречается в выборке чаще всего;

мощность критерия:вероятность правильного отклонения нулевой гипотезы при условии справедливости альтернативной гипотезы. Равна 1 – β, где β – вероятность ошибки второго рода для статистического критерия;

мудрость толпы:идея, согласно которой характеристика, определяемая групповым мнением, ближе к истине, чем предположения большинства отдельных людей;

наука о данных:изучение и применение методов получения информации из данных, включая построение алгоритмов для прогнозов. Традиционная статистика – часть науки о данных, в которую также входят кодирование и управление данными;

независимая (предикторная) переменная:переменная, которая фиксируется посредством проекта или наблюдения, чья связь с зависимой переменной может представлять интерес;

независимые события:события A и B независимы, если наступление A не влияет на вероятность наступления B , то есть ( B | A ) = p ( B ), или, что эквивалентно, p ( BA ) = p ( B ) p ( A ) [280];

непрерывная случайная величина:случайная величина X , которая может (по крайней мере, в принципе) принимать любое значение в пределах определенного промежутка. Непрерывная величина имеет плотность вероятности [281] – такая функция ƒ, что 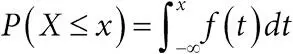, а ее математическое ожидание определяется формулой 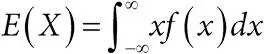. Вероятность того, что X попадет в промежуток ( A,B ), равна ;

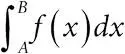нормальное распределение:случайная величина имеет нормальное (гауссовское) распределение со средним μ и дисперсией σ 2, если ее плотность имеет вид

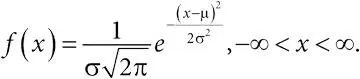
Математическое ожидание E ( X ) = μ, дисперсия D ( X ) = σ 2, среднеквадратичное отклонение SD ( X ) = σ.

Стандартизованная случайная величина 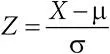имеет среднее 0 и дисперсию 1, и тогда говорят, что у нее стандартное нормальное распределение. Функцию распределения для стандартной нормальной величины Z обозначают Φ. Например, Φ(–1) = 0,16 – это вероятность того, что стандартная гауссовская случайная величина не превосходит –1, или (что эквивалентно) вероятность того, что произвольная гауссовская случайная величина с параметрами μ и σ принимает значение, которое меньше μ−σ·100 p %.% процентиль для стандартного нормального распределения – такое число z p , что P ( Z ≤ z p ) = p . Как значения функции Φ, так и величины z p можно найти в таблицах или в стандартных программах: например, 75-й процентиль для стандартного нормального распределения равен z 0,75 = 0,67;