Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных

возмущающий (искажающий) фактор:переменная, которая связана и с предикторной переменной, и с переменной отклика и может объяснить часть их видимой взаимосвязи. Например, рост и вес детей сильно коррелированы, но в основном эта взаимосвязь объясняется возрастом ребенка;

воронкообразный график:график, где наблюдениям, соответствующим отдельным элементам (учреждения, области или исследования), сопоставляется мера их точности. Часто две «воронки» указывают на то, где можно ожидать месторасположения 95 % и 99,8 % наблюдений, когда между элементами в действительности нет разницы. Если распределение наблюдений приближенно нормальное, то граничные значения для 95 % и 99,8 % примерно соответствуют ±2 и ±3 стандартным ошибкам;

выборочное среднее:см. среднее 2.

генеральная совокупность (популяция):группа, из которой, как предполагается, берутся данные в выборке и которая дает вероятностное распределение для отдельного наблюдения. При проведении измерений или наличии у вас всех возможных данных это понятие становится математической идеализацией;

глубокое обучение:метод машинного обучения, который расширяет стандартные модели искусственных нейронных сетей на множество слоев, представляющих различные уровни абстракции, например переход от отдельных пикселей изображения к распознанию объектов;

гипергеометрическое распределение:пусть имеется конечное множество из N элементов, K из которых обладают некоторым свойством. Мы выбираем n элементов без возвращения. Тогда случайная величина Y – число успехов (выбранных элементов с этим свойством) имеет гипергеометрическое распределение. Формально для k = 0,1,…, n

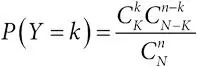
грамотность в работе с данными:умение понимать принципы, лежащие в основе работы с данными, выполнять базовые анализы данных, критически анализировать качества утверждений, сделанных на основе данных;

дерево классификации:форма алгоритма классификации, при котором характеристики проверяются последовательно; ответ на очередной вопрос определяет, какая характеристика проверяется следующей; процедура повторяется до итоговой классификации;

дилемма смещения – дисперсии:когда для прогноза используется обучение модели, повышение ее сложности в итоге приводит к тому, что у модели уменьшается смещение (в том смысле, что у нее возрастает потенциал для адаптации к деталям базового процесса), но увеличивается дисперсия, поскольку данных для уверенности в параметрах модели оказывается недостаточно. Чтобы избежать переобучения, нужен компромисс;

дисперсия выборочная:если имеется выборка x 1, x 2,…, x n со средним 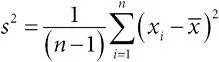, то выборочная дисперсия (хотя знаменатель может быть равен n , а не n −1) [279];

дисперсия:характеристика разброса случайной величины; если случайная величина X имеет математическое ожидание E ( X ) = μ, то дисперсия D ( X ) = E ( X −μ) 2Среднеквадратичное (стандартное) отклонение является корнем из дисперсии, так что ;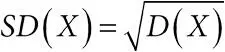

доверительный интервал:оцениваемый интервал, в котором может находиться неизвестный параметр. Например, при наличии наблюдаемого множества данных x 95-процентный доверительный интервал для среднего μ – это такой интервал от L ( x ) до U ( x ), когда до наблюдения данных вероятность того, что случайный интервал ( L ( x ), U ( x )) содержит μ, составляет 95 %. Если соединить центральную предельную теорему с тем фактом, что примерно 95 % нормального распределения отклоняется от среднего не более чем на 2 стандартных отклонения, мы получим популярное приближение, что 95-процентный доверительный интервал – это оценка в ±2 стандартные ошибки. Предположим, что мы хотим найти доверительный интервал для разности μ 2−μ 1между двумя параметрами μ 2и μ 1. Если T 1 – это оценка для μ 1со стандартной ошибкой SE 2, а T 2 – это оценка для μ 2со стандартной ошибкой SE 2, то T 2− T 1представляет собой оценку для μ 2−μ 1. Дисперсия разности между оценками равна сумме их дисперсий, и поэтому стандартная ошибка для T 2− T 1 определяется формулой 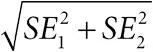. Отсюда можно найти 95-процентный доверительный интервал для разности μ 2−μ 1;

зависимая переменная (переменная отклика):переменная, которая представляет основной интерес, которую мы желаем спрогнозировать или объяснить;

зависимые события:когда вероятность одного события зависит от наступления другого;

закон больших чисел:общее название нескольких теорем о сходимости средних для последовательности случайных величин к истинному математическому ожиданию. На практике это означает, что выборочное среднее близко к среднему значению всей генеральной совокупности;

иерархическое моделирование:в байесовском анализе – когда параметры, определяющие число элементов (например, районов или школ), сами считаются взятыми из общего априорного распределения. Это приводит к уменьшению оценок параметров для отдельных элементов в сторону общего среднего;

индуктивное поведение:сделанное в 1930-х годах предложение Ежи Неймана и Эгона Пирсона по проверке гипотез в терминах принятия решений. От него остались идеи размера и мощности критерия, а также ошибок первого и второго рода;

индукция (индуктивное умозаключение):построение обобщающего вывода на основании частных примеров;

интерквартильный размах:мера разброса выборки или распределения; конкретно – разность между третьим и первым квартилем, то есть между 75-м и 25-м процентилем;

искусственный интеллект (ИИ):компьютерные программы, предназначенные для выполнения задачи, обычно связываемой с человеческими способностями;

исследование «случай – контроль»:ретроспективное исследование, в котором люди с заболеванием или с интересующей нас характеристикой (случаи) сопоставляются с одним или несколькими людьми, не имеющими заболевания (контрольные экземпляры), и сравниваются истории этих групп – чтобы увидеть, дают ли воздействия систематическую разницу между группами. Такая схема может оценивать только относительные риски, связанные с воздействиями;