Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных
- Название:Искусство статистики. Как находить ответы в данных
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2021
- Город:Москва
- ISBN:9785001692508
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных краткое содержание
Эта книга предназначена как для студентов, которые хотят ознакомиться со статистикой, не углубляясь в технические детали, так и для широкого круга читателей, интересующихся статистикой, с которой они сталкиваются на работе и в повседневной жизни. Но даже опытные аналитики найдут в книге интересные примеры и новые знания для своей практики. На русском языке публикуется впервые.
Искусство статистики. Как находить ответы в данных - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
калибровка:требование, чтобы наблюдаемые частоты событий соответствовали вероятностным прогнозам. Например, если вероятность какого-нибудь события 0,7, то оно должно происходить примерно в 70 % случаев;
качественная (категорийная) переменная: переменная, принимающая два или несколько дискретных значений, которые могут или не могут быть упорядоченными;
квартиль (генеральной совокупности):25-й, 50-й и 75-й процентили;
комбинированные признаки:когда несколько объясняющих переменных соединяются и производят эффект, отличный от ожидаемого при их отдельном воздействии;
конструирование признаков:в машинном обучении процесс уменьшения размерности входных переменных с созданием сводных характеристик, которые содержат информацию о данных в целом;
контрольная группа:множество людей, которые не подпадали под интересующее нас воздействие;
контрольные граничные значения:заранее определенные ограничения для случайной величины, используемые при контроле качества для отслеживания отклонений от предполагаемых стандартов; например, могут отображаться на воронкообразном графике;
контрфактуальный:относящийся к сценариям вида «что, если», где рассматривается альтернативная история событий;
коэффициент регрессии:оцениваемый параметр в статистической модели, который выражает степень взаимосвязи между объясняющей переменной и результатом во множественной регрессии. Этот коэффициент будет иметь различную интерпретацию в зависимости от того, является ли результирующая переменная непрерывной (множественная линейная регрессия), долей (логистическая регрессия), целым числом (пуассоновская регрессия) или временем выживания (регрессия Кокса);
кризис воспроизводимости:утверждение, что многие опубликованные научные выводы основаны на недостаточно качественных работах, поэтому такие результаты не могут воспроизвести другие исследователи;
критерий независимости хи-квадрат/критерий согласия хи-квадрат:статистический критерий, показывающий степень несовместимости данных с принятой статистической моделью, заключающей нулевую гипотезу (например, величины независимы или имеют определенное распределение). А именно: критерий сравнивает множества каких-то наблюдаемых величин x 1,…, x m и ожидаемых при нулевой гипотезе величин y 1,…, y m . Простейший вариант критерия –
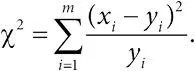
При нулевой гипотезе значение χ 2приближенно будет иметь известное χ 2-распределение. Это позволяет вычислить соответствующее P-значение;
логарифмическая шкала:логарифм по основанию 10 для положительного числа x обозначается y = log 10 x , что эквивалентно x = 10 y . В статистическом анализе log x обычно обозначает натуральный логарифм log e x , что эквивалентно x = e y , где e – основание натурального логарифма 2,71828…;
логистическая регрессия:форма множественной регрессии, когда переменная отклика – это доля, а коэффициенты соответствуют log(отношение шансов). Допустим, мы наблюдаем набор долей y i = r i / n i в предположении, что у нас биномиальные величины с вероятностями p i , а соответствующий набор предикторных переменных – 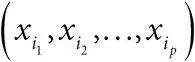 . Предполагается, что логарифм шансов с оцениваемой вероятностью
. Предполагается, что логарифм шансов с оцениваемой вероятностью 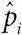 определяется линейной регрессией:
определяется линейной регрессией:
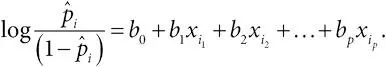
Допустим, что одна из предикторных переменных, например x 1, является двоичной, где x 1 = 0 соответствует отсутствию воздействия потенциального риска, а x 1 = 1 соответствует воздействию. Тогда коэффициент b 1 – это log(отношение шансов);
ложноположительный:неверная классификация «отрицательного» случая как «положительного»;
математическое ожидание (среднее):среднее значение случайной величины (взвешенное по вероятностям или по плотности). Для дискретной случайной величины это ∑ xp ( x ), а для непрерывной случайной величины это ∫ xp ( x ) dx . Например, если случайная величина X – это число очков, выпавших на симметричной игральной кости, то есть P ( X = x ) = 1/6 для x = 1,2,3,4,5,6, то 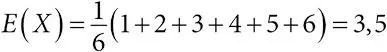 ;
;
матрица ошибок:таблица, где собраны верные и неверные классификации, произведенные каким-либо алгоритмом;
машинное обучение:процедуры извлечения алгоритмов (например, для классификации, прогнозирования или кластеризации) из сложных данных;
медиана (выборки):значение, которое окажется посередине, если упорядочить числа в выборке. Более строго: упорядочив числа в выборке, обозначим наименьшее число x (1), второе по величине x (2)и так далее (получившийся набор x (1), x (2),…, x (n)называют вариационным рядом). Если n – нечетное число, то медиана – число, находящееся точно посередине вариационного ряда, то есть число 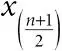 . Если же n – четное число, то медианой обычно считают полусумму двух средних чисел;
. Если же n – четное число, то медианой обычно считают полусумму двух средних чисел;
метаанализ:формальный статистический метод объединения результатов нескольких исследований;
метод наименьших квадратов:предположим, что у нас есть n пар чисел ( x 1, y 1),( x 2, y 2), 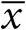 , s x – выборочное среднее и среднеквадратичное отклонение для чисел x и
, s x – выборочное среднее и среднеквадратичное отклонение для чисел x и 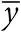 s y – выборочное среднее и среднеквадратичное отклонение для чисел y . Тогда прямая регрессии, вычисленная по методу наименьших квадратов, определяется уравнением
s y – выборочное среднее и среднеквадратичное отклонение для чисел y . Тогда прямая регрессии, вычисленная по методу наименьших квадратов, определяется уравнением
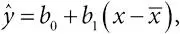
где
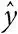 – прогнозируемое значение зависимой переменной для определенного значения независимой переменной x ;
– прогнозируемое значение зависимой переменной для определенного значения независимой переменной x ;
коэффициент наклона 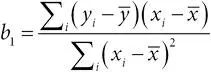 ;
;
Интервал:
Закладка:








