Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

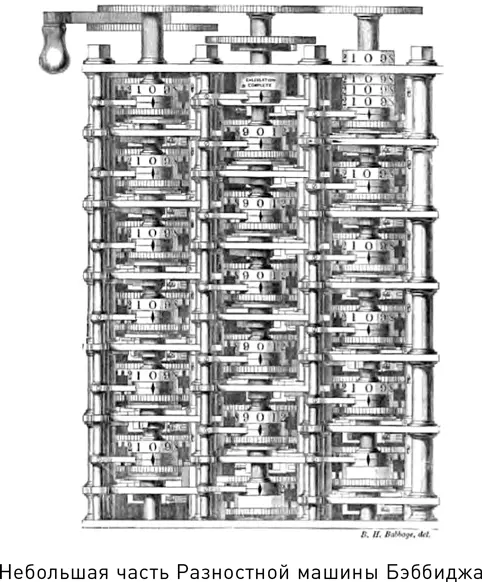
Его первую попытку двигаться в этом направлении – Разностную машину – правильнее всего рассматривать как механический предвестник знакомого всем калькулятора; он мог выполнять основные действия арифметики. Его главной задачей было вычисление полиномиальных функций, таких как квадраты и кубы, или более сложные формы, методами исчисления конечных разностей.

Основная идея проста. Закономерности в этих функциях проявляются, если рассматривать разности между последовательными величинами. К примеру, начнем с кубов:

0 1 8 27 64 125 216.

Разности между последовательными числами выглядят так:

1 7 19 37 61 91.

Возьмем разности еще раз:

6 12 18 24 30.

И еще:

6 6 6 6.

После этого простая закономерность становится очевидной. (Она очевидна, строго говоря, уже на предыдущем шаге; и на предпредыдущем, хотя и в меньшей степени.) Эта закономерность по-настоящему важна, поскольку дает возможность просчитать весь процесс в обратном порядке. Итоговая серия шестерок позволяет восстановить последовательность непосредственно перед ней; суммирование получившихся чисел дает предыдущую последовательность; наконец, суммирование этой последовательности дает кубы. Аналогичный метод работает для любой полиномиальной функции. Нужно только уметь складывать. В умножении, которое представляется более сложным, необходимости нет.

Идею привлечения к вычислениям механических помощников трудно назвать новой. В истории математики наблюдается давняя традиция привлечения к процессу счета подобных помощников, начиная со счета на пальцах и заканчивая компьютером. Но план Бэббиджа отличался необычной амбициозностью. Обнародовал он эту идею в работе, представленной в Королевском астрономическом обществе в 1822 г., а годом позже получил от британского правительства 1700 фунтов на пилотный проект. К 1842 г. инвестиции правительства выросли до 17 000 фунтов (в сегодняшних деньгах это примерно три четверти миллиона фунтов – $1 млн), при том что реальной работающей машины так и не появилось. Ада и ее мать в 1833 г. видели прототип – небольшую часть проекта. Что еще хуже (с точки зрения правительства), Бэббидж после почти 20 лет работы предложил еще более амбициозный проект – Аналитическую машину, настоящий программируемый компьютер, построенный из хитроумно устроенных штырьков, рычажков, пружинок и храповичков. Эта машина положила начало целому жанру научной фантастики – так называемому стимпанку, где действуют механические версии всего на свете, от компьютеров до мобильных телефонов и интернета. Как ни печально, и Разностная, и Аналитическая машины навсегда остались научной фантастикой. Однако уже в наше время Разностная машина была построена в Лондонском музее науки; руководил проектом Дорон Суэйд. Машина, построенная по второму проекту Бэббиджа, работает; ее можно сегодня осмотреть в музее. Другая машина, построенная по первому проекту Бэббиджа, находится в Музее истории компьютера в Калифорнии. Построить Аналитическую машину никто пока не пытался.

В 1834 г. Ада встретилась с одной из великих женщин-математиков Мэри Сомервиль, близким другом Бэббиджа. Вдвоем они провели немало часов за разговорами о математике; Мэри одалживала Аде учебники и предлагала задачи для решения. Говорили они и о Бэббидже с его Разностной машиной. Две женщины подружились и вместе ходили не только на научные демонстрации, но и, к примеру, на концерты.

В 1835 г. Ада вышла замуж за Уильяма Кинга-Ноэля, ставшего через три года первым графом Лавлейсом. У супругов родилось трое детей, после чего Ада вернулась к своей первой любви – математике, которой и стала заниматься под руководством известного математика, логика и оригинала Огастеса де Моргана, основателя Лондонского математического общества и грозы математических фриков. В 1843 г. она начала тесно сотрудничать с Бэббиджем; их сотрудничество выросло из репортажа о лекции про Аналитическую машину, прочитанной Бэббиджем в Турине в 1840 г. Луиджи Менабреа сделал на лекции записи и собрал их для публикации. Ада перевела их с итальянского, и Бэббидж предложил ей написать к заметкам собственный комментарий. Она согласилась с энтузиазмом, и очень скоро ее комментарий превзошел саму лекцию.

Результат этих трудов был опубликован в серии «Научные мемуары», которую издавал Ричард Тейлор. На последней стадии подготовки книги к печати Бэббидж вдруг передумал: он решил, что комментарий Ады настолько хорош, что лучше было бы ей издать его отдельно в виде книги. Леди Кинг весьма аристократично возмутилась: большая часть уже сделанной работы пропадет, печатник будет недоволен нарушением контракта – нет, это нелепая идея. Бэббидж тут же сдал назад; она, конечно, заранее понимала, что он отступит. Чтобы смягчить удар, Ада предложила и дальше писать о его работе – при условии, что подобных конфликтов больше не будет. Она намекнула также, что сможет, наверное, помочь с получением финансирования для постройки Аналитической машины, если Бэббидж соберет группу практичных друзей, которые могли бы следить за проектом и контролировать его ход. Мать Ады всегда жаловалась на болезни и плохое самочувствие; предлагая это, Ада, возможно, имела в виду свое возможное наследство. Если так, ее ждало разочарование, ибо в конечном итоге мать пережила ее на восемь лет.

Комментарий Ады – главный документ, на котором зиждется ее научная репутация. В нем не только объясняется принцип действия устройства, но и вносятся два существенных новшества в то, что мы сегодня рассматриваем как развитие компьютера.

Во-первых, Ада проиллюстрировала гибкость будущей машины. Если Разностная машина представляла собой калькулятор, то Аналитическая была уже настоящим компьютером, способным исполнять программы, при помощи которых можно было посчитать что угодно и, более того, выполнить любой заданный алгоритм. Сама идея принадлежала Бэббиджу, но Ада предложила серию иллюстративных примеров, показывавших, как можно настроить машину на выполнение конкретных вычислений. Самым амбициозным из примеров было получение так называемых чисел Бернулли. Эти числа названы так в честь Якоба Бернулли, который написал о них в своем трактате «Искусство предположений» (Ars Conjectandi, 1713 г.) – одной из первых книг по комбинаторике и теории вероятностей. Японский математик Секи Кова открыл их раньше, но его результаты были опубликованы лишь после его смерти. Эти числа возникают при разложении в ряд тригонометрической функции тангенса и встречаются также в некоторых других математических контекстах. Все они представляют собой рациональные числа (дроби), и каждое второе число Бернулли, начиная с третьего, равно нулю; помимо этого, в них не наблюдается никаких очевидных закономерностей. Вот первые несколько чисел: